運動学と力学の基本的な物理量の定義
運動学とは力学の分野の内で「物体の運動を時間や空間の観点から記述する学問」であり、力などの作用については言及しない分野です。
まずは力学の基本的な物理量である
・位置ベクトル $\vec{r}$
・速度ベクトル $\vec{v}$
・加速度ベクトル $\vec{a}$
の定義を確認しておきましょう。
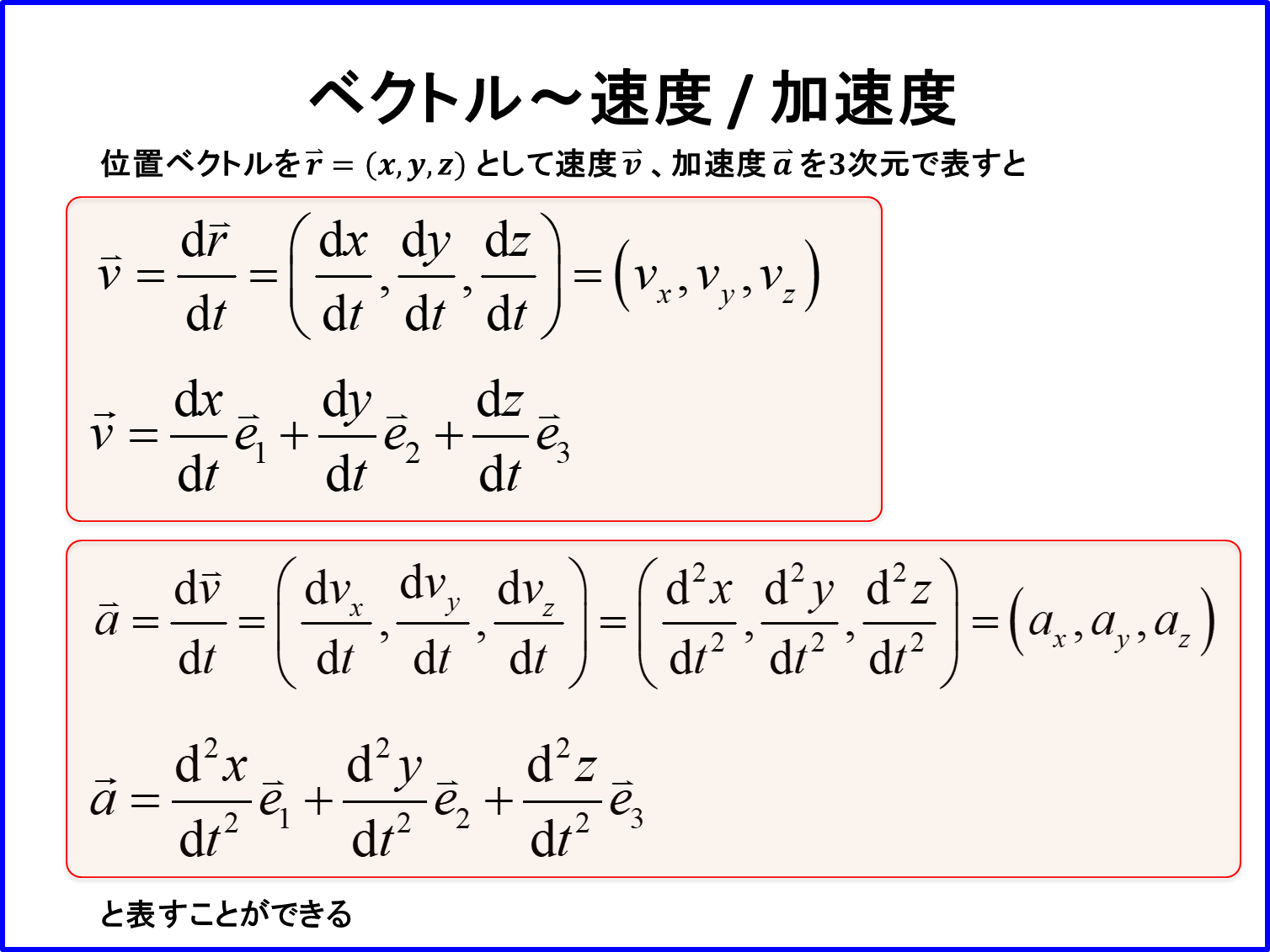
速度ベクトル$\vec{v}$
位置ベクトル$\vec{r}$を$\vec{r}=(x, y, z)$とすると
「速度ベクトル$\vec{v}$は位置ベクトル$\vec{r}$の時間微分」で定義され、
\begin{eqnarray*}
\vec{v} = \frac{\diff \vec{r}}{\diff t}
\end{eqnarray*}
となります。
$\vec{r}$は$3$成分を持っているので
\begin{eqnarray*}
\vec{v} = \frac{\diff \vec{r}}{\diff t} = \frac{\diff }{\diff t} (x, y, z)
\end{eqnarray*}
であり
\begin{eqnarray*}
\vec{v} = \biggl( \frac{\diff x}{\diff t} , \frac{\diff y}{\diff t} , \frac{\diff z}{\diff t}\biggr)
\end{eqnarray*}
と表すことができます。
それぞれの成分の速度を表すために添え字を用いて表すと
\begin{eqnarray*}
\vec{v} = (v_x, v_y, v_z)
\end{eqnarray*}
と表すことになります。
又、単位ベクトルを用いて各成分の和の形の式で表すこともできます。
加速度ベクトル$\vec{a}$
続いて、「加速度ベクトル$\vec{a}$は速度ベクトル$\vec{v}$の時間微分」で定義され、
\begin{eqnarray*}
\vec{a} = \frac{\diff \vec{v}}{\diff t}
\end{eqnarray*}
となります。
従って、
\begin{eqnarray*}
\vec{a} = \frac{\diff \vec{v}}{\diff t} = \frac{\diff }{\diff t} (v_x, v_y, v_z) = \biggl( \frac{\diff v_x}{\diff t} , \frac{\diff v_y}{\diff t} , \frac{\diff v_z}{\diff t}\biggr)
\end{eqnarray*}
と表すことができます。
ここで、$\vec{v}=(v_x, v_y, v_z)$は$\vec{r}$を微分したものなので
\begin{eqnarray*}
\vec{a} = \biggl( \frac{\diff v_x}{\diff t} , \frac{\diff v_y}{\diff t} , \frac{\diff v_z}{\diff t}\biggr)
&=&
\biggl( \frac{\diff }{\diff t} \biggl( \frac{\diff x}{\diff t} \biggr), \frac{\diff }{\diff t} \biggl( \frac{\diff y}{\diff t} \biggr) , \frac{\diff }{\diff t} \biggl( \frac{\diff z}{\diff t} \biggr) \\
\\
&=& \biggl( \frac{\diff^2 x}{\diff t^2} , \frac{\diff^2 y}{\diff t^2} , \frac{\diff^2 z}{\diff t^2}\biggr)
\end{eqnarray*}
となり$\vec{r}$の2階微分という形で表されています。
又、添え字を用いた表現や単位ベクトルを用いた表現も速度ベクトルの時と同様に使用できます。
ここで着目するべきは、直交座標軸であれば速度ベクトル$\vec{v}$も加速度ベクトル$\vec{a}$もそれぞれ成分ごとに分かれていてお互いに干渉しない点になります。(極座標軸を用いる場合は別になるので注意が必要)
それぞれの成分ごとに考えれば良いことになります。
一次元の例
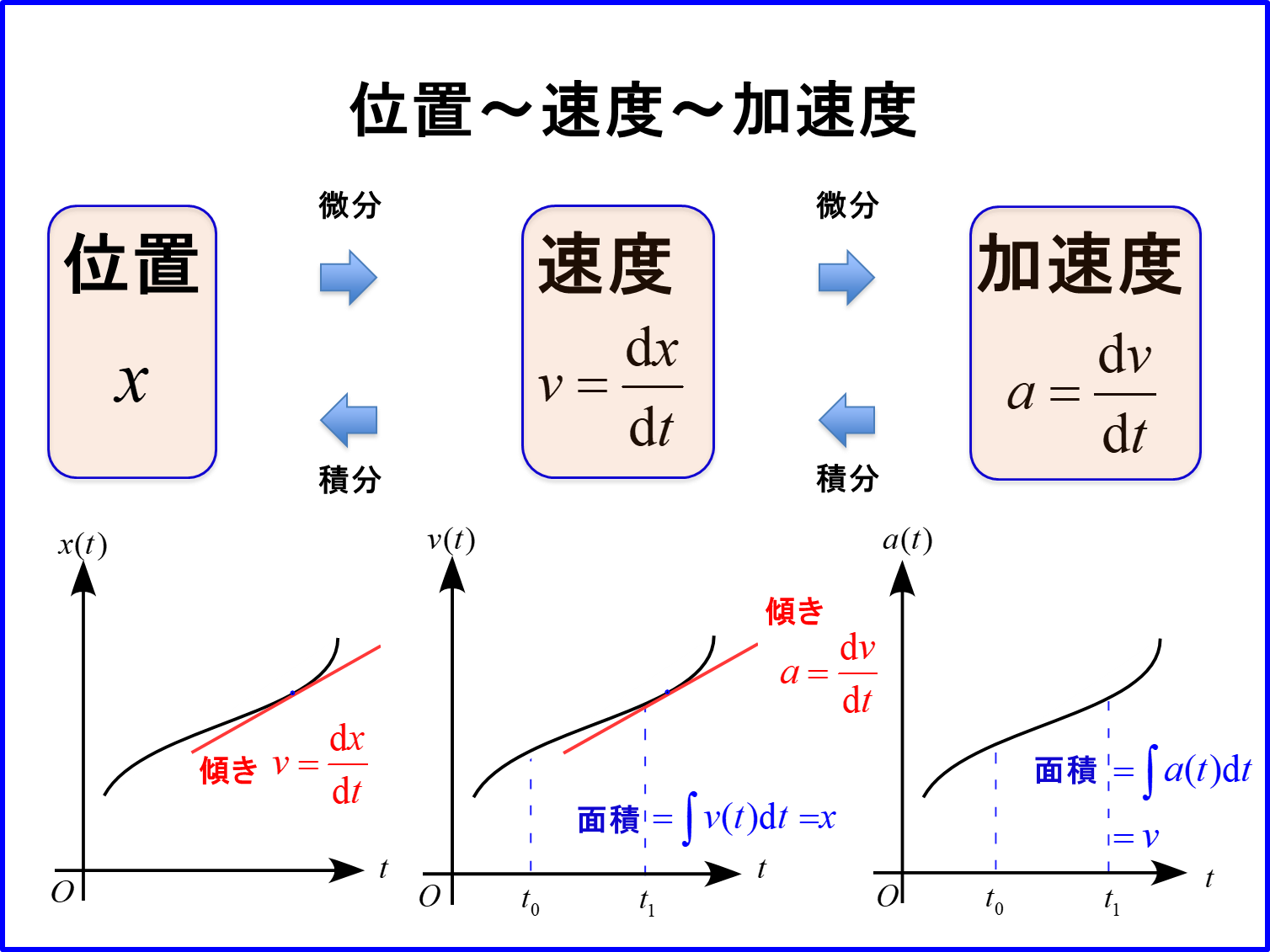
一次元の例として、$x$成分に着目すると
位置$x$、速度$v$、加速度$a$は図の様に微分・積分の関係であり、計算によって他の物理量を求めることができます。
又、グラフを描くことによりそれぞれの関係が視覚的に解り、理解がすすみます。
具体的な手順としては
・条件を書き出す
・$v-t$グラフを描く
・定義に沿って求められた物理量を計算する
で進めて行きます。
物理現象として何が起こっているのかを把握するためには初期条件や運動の条件などを抜き出して書き出すことが重要です。
そして、$v-t$グラフを描くことをお勧めします。
もちろん、$x-t, v-t, a-t$グラフを全て描けば良いのですが、手間と時間の都合もあるので描かない場合の最優先は$v-t$グラフです。
$v-t$グラフの傾きは加速度$a$を表し、$v-t$グラフと時間軸$t$で囲む面積は変位(位置)を表すので、$v-t$グラフは最重要になります。
条件とグラフが出来てしまえば、それぞれの関係式から計算すれば求めたい物理量を得ることができます。
等加速度運動の公式とか気にする必要はありません。もちろん、知っていれば答えが速く求まることがあるかもしれませんが、その程度です。
物理量の定義を押さえることの方が大事です。
力学の手順
続いて、力学の手順です。
ここからは力の作用を考えることになります。
慣れるまで手順に沿って進めましょう。
運動方程式を立てる
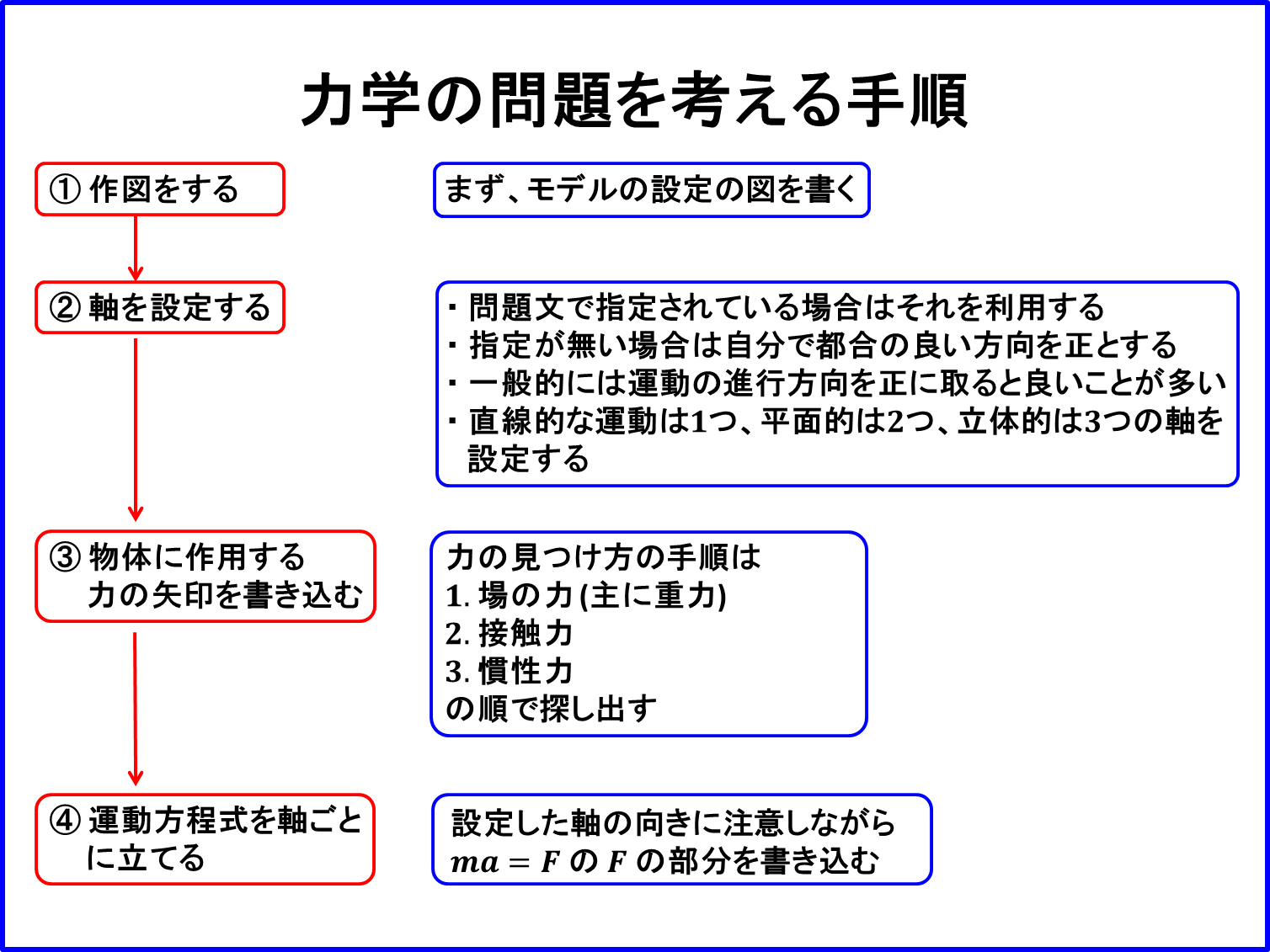
まず、「作図をする」ことです。
考えるモデルの絵を描きます。
問題となっているモデルの現象を図で表すことができないとその先のステップに進めません。適当に公式を覚えたところで理解にはつながりません。
その「モデルがどのような状況であるかの図」を描きましょう。
続いて、「軸の設定」です。この軸の設定は重要です。
作図したモデル図に座標軸を記入します。
この「軸の向きの設定」によって「正負」が決まります。
軸の設定は、本来自由です。軸の設定によって物理現象が変わってしまうことはありません。(軸を上向きに設定しても、下向きに設定しても自由落下なら物体は下に落ちます。物理現象が変わることはありません。)
しかし、問題等で指定されている場合はそれを利用します。
出題者に逆らってもあまりよいことはありません。
仮に、別軸の設定で解いたとしても最後は出題の設定に戻す必要が出て面倒なことになります。
指定が無い場合は、自分で設定することになります。
一般的には「運動の進行方向を正に設定する」と良い場合が多いですが、絶対ではありません。
軸はモデルの運動に合わせて$1-3$次元まで設定しましょう。
次のステップは「物体に作用する力の矢印を書き込む」ことです。
物体に作用する力を「場の力, 接触力, 慣性力」の順で探し出し、
モデル図に矢印を書き込みましょう。
矢印を書いた後、「何の力」かが判るように「力の大きさ」も書き加えましょう。
最後に、「運動方程式を軸ごとに立てる」ことになります。
設定した軸の向きに注意しながら$ma=F$の$F$の部分を書き込んでいきます。
前のステップで記入した力の矢印が軸に沿っていない場合は力の矢印の成分の分解が必要になります。
ここまでが、運動方程式を立てる手順になります。
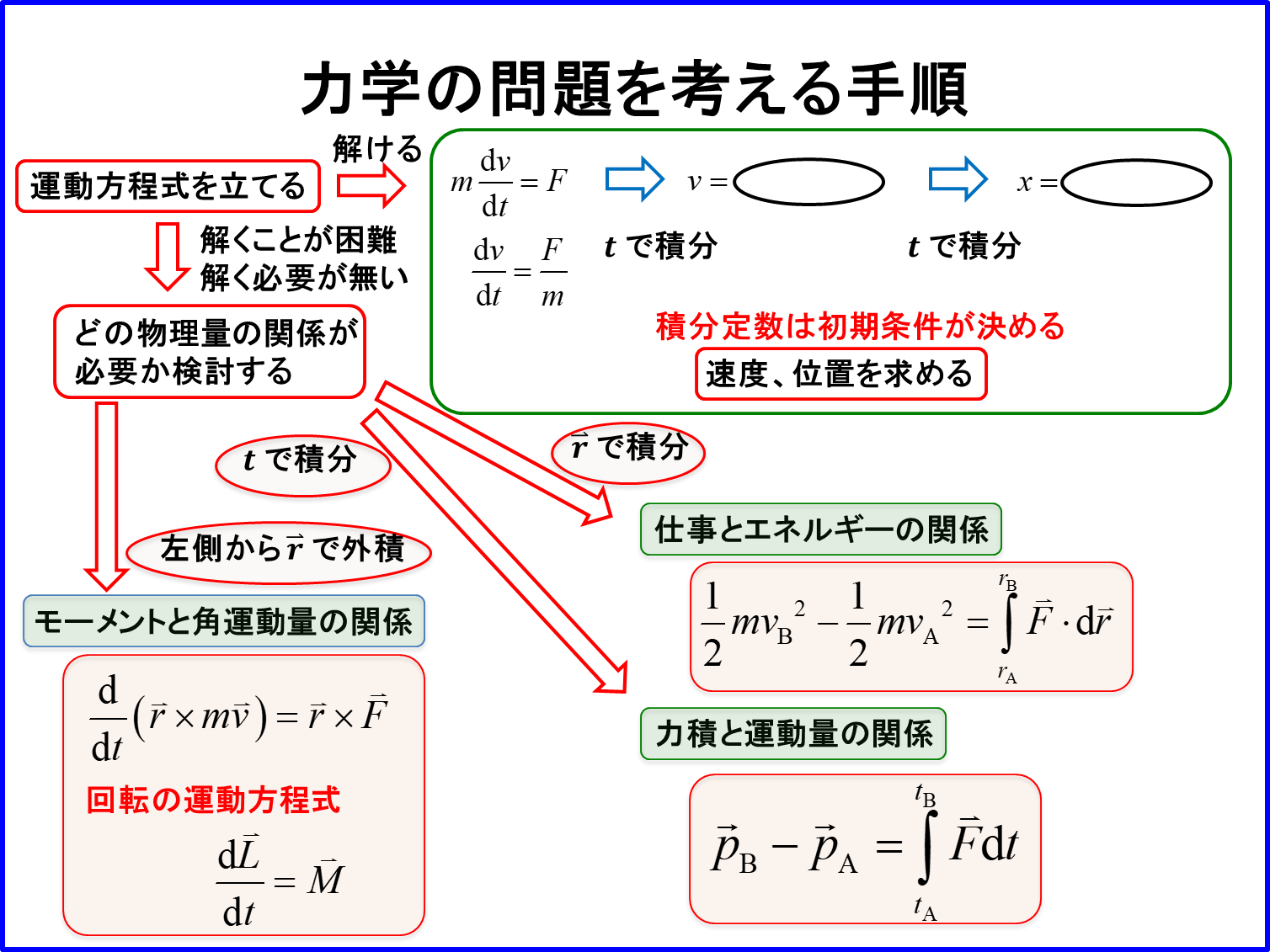
運動方程式の活用
運動方程式が出来た後は、この「運動方程式を解くかどうか」の検討を行います。
「すぐ解ける場合」は加速度$\displaystyle \frac{\diff v}{\diff t}=\frac{F}{m}$の形に変形し、$t$で積分して速度$v$を計算し、さらに$t$で積分して位置$x$を計算します。
この積分は不定積分となるので、積分定数の処理をきちんと行う必要があります。
積分定数は初期条件などにより決定できます。
「解くことが困難な場合」あるいは「解かない方が早い場合」「解く必要が無い場合」はどの物理量の関係が求められているのかを検討します。
運動方程式を$\vec{r}$で積分することで、つまり距離積分で「仕事とエネルギーの関係式」が導かれます。
運動方程式を$t$で積分することで、つまり時間積分で「力積と運動量の関係式」が導かれます。
さらに、運動方程式を左から位置ベクトル$\vec{r}$で外積を取ることで「モーメントと角運動量の関係式」が導かれます。
いずれも、左辺に$\displaystyle \frac{\diff}{\diff t} \bigl(\quad \bigr)$の形、つまり時間変化に着目した形を作り、右辺はその結果で構成された物理量と解釈することもできます。
それぞれ問われている物理量の関係式を利用し、必要な物理量を求めることになります。
この流れを頭に入れておくと、解法の全体像が見えてきます。