問題
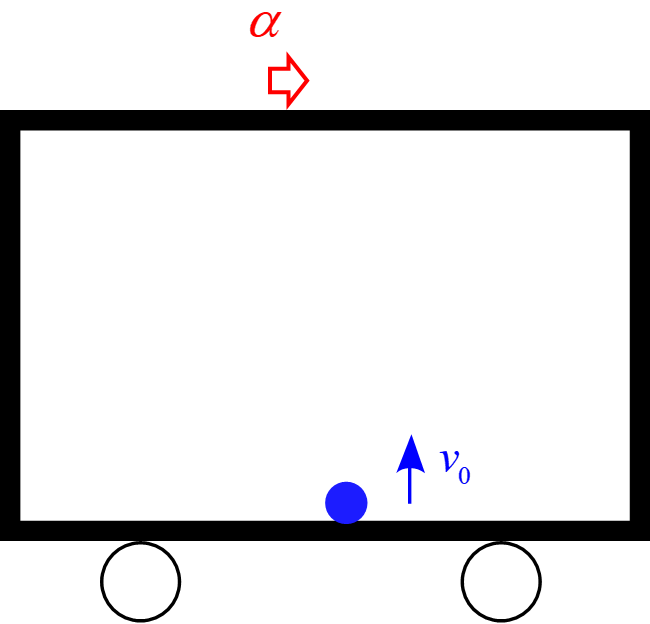
電車が一定の加速度$\alpha$で水平右向きに進んでいる。この電車内で、質量$m$の物体を初速度$v_0$で床から鉛直に投げ上げた。以下の問いに答えよ。
(1) 物体の運動方程式を記述せよ。
(2) 速度$v_x(t), v_y(t)$及び位置$x(t), y(t)$を表せ。
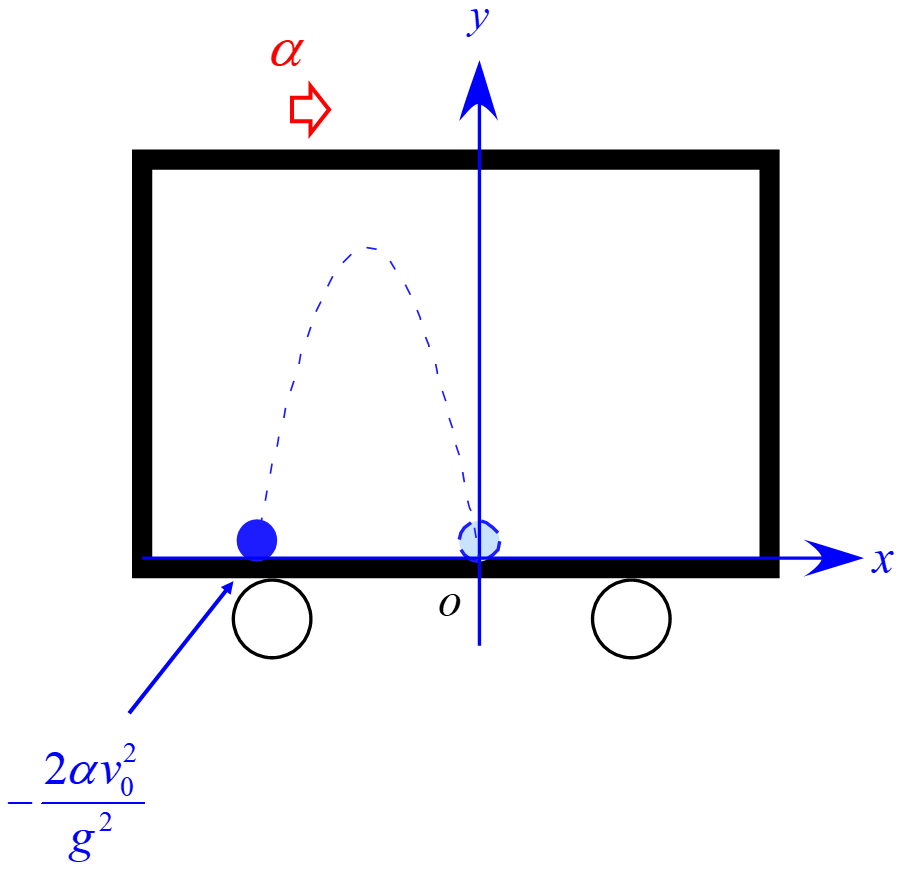
(3) 再び床に戻ったときの位置を求めよ。
解答
(1)
電車内に座標軸を設定すると物体に作用する力は場の力「重力$mg$」と慣性力「$m\alpha$」となる。
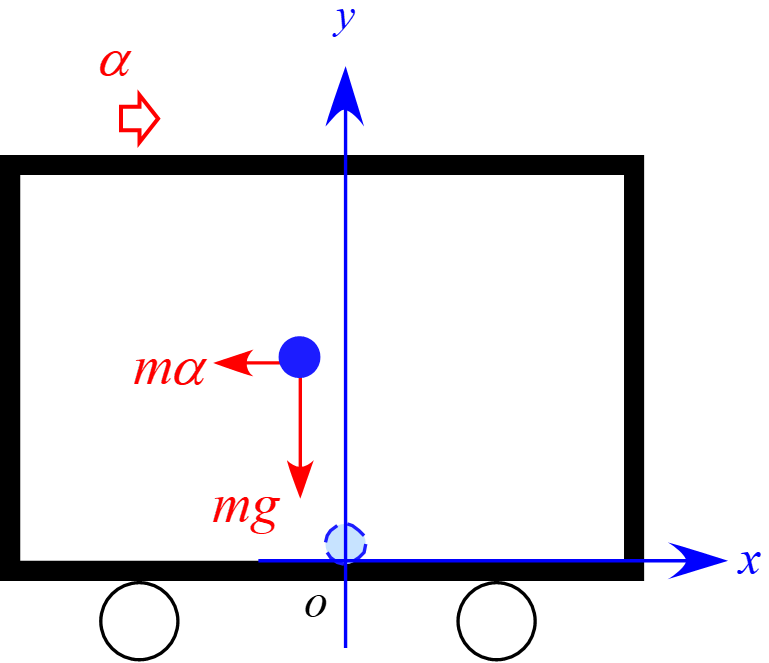
従って、運動方程式は
\begin{eqnarray*}
m a_x &=& - m \alpha \\
\\
m a_y &=& -mg
\end{eqnarray*}
となる。
(2)
運動方程式より加速度は
\begin{eqnarray*}
a_x &=& - \alpha \\
\\
a_y &=& -g
\end{eqnarray*}
と表される。
$x$軸について速度$v_x$と位置$x$を求めると、
\begin{eqnarray*}
a_x = \frac{\diff v_x}{\diff t} &=& - \alpha \\
\\
\int \frac{\diff v_x}{\diff t} \diff t&=& \int (- \alpha)\ \diff t \\
\\
\int \diff v_x&=& \int (- \alpha)\ \diff t \\
\\
v_x&=& - \alpha t+C_1 \qquad (C_1: \mbox{積分定数}) \\
\end{eqnarray*}
となり、初期条件$v_x(0)=0$より
\begin{eqnarray*}
v_x (0) = - \alpha \cdot 0+C_1 &=& 0\\
\\
C_1 &=& 0
\end{eqnarray*}
となるので、
\begin{eqnarray*}
v_x (t) = - \alpha t\\
\end{eqnarray*}
となる。
さらに$t$で積分すると
\begin{eqnarray*}
v_x (t) = \frac{\diff x}{\diff t} &=& - \alpha t\\
\\
\int \frac{\diff x}{\diff t} \diff t &=& \int (- \alpha t)\ \diff t\\
\\
\int \diff x &=& \int (- \alpha t)\ \diff t \\
\\
x &=& - \frac{1}{2} \alpha t^2+C_2 \qquad (C_2: \mbox{積分定数}) \\
\end{eqnarray*}
となり、原点スタートとすると$x(0)=0$より
\begin{eqnarray*}
x (0) = - \frac{1}{2} \alpha \cdot 0^2+C_2 &=& 0 \\
\\
C_2 &=&0
\end{eqnarray*}
となるので、
\begin{eqnarray*}
x (t) = - \frac{1}{2} \alpha t^2\\
\end{eqnarray*}
となる
一方、$y$軸について速度$v_y$と位置$y$を求めると、
\begin{eqnarray*}
a_y = \frac{\diff v_y}{\diff t} &=& - g \\
\\
\int \frac{\diff v_y}{\diff t} \diff t&=& \int (- g)\ \diff t \\
\\
\int \diff v_y&=& \int (- g)\ \diff t \\
\\
v_y&=& - g t+C_3 \qquad (C_3: \mbox{積分定数}) \\
\end{eqnarray*}
となり、初期条件$v_y(0)=v_0$より
\begin{eqnarray*}
v_y (0) = - g \cdot 0+C_1 &=& v_0\\
\\
C_1 &=& v_0
\end{eqnarray*}
となるので、
\begin{eqnarray*}
v_y (t) = - g t +v_0 \\
\end{eqnarray*}
となる。
さらに$t$で積分すると
\begin{eqnarray*}
v_y (t) = \frac{\diff y}{\diff t} &=& - g t +v_0\\
\\
\int \frac{\diff y}{\diff t} \diff t &=& \int (- g t +v_0)\ \diff t\\
\\
\int \diff y &=& \int (- g t +v_0)\ \diff t \\
\\
y &=& - \frac{1}{2} g t^2 +v_0 t+C_4 \qquad (C_4: \mbox{積分定数}) \\
\end{eqnarray*}
となり、原点スタートとすると$y(0)=0$より
\begin{eqnarray*}
y (0) = - \frac{1}{2} g \cdot 0^2 +v_0 \cdot 0+ C_4 &=& 0 \\
\\
C_4 &=&0
\end{eqnarray*}
となるので、
\begin{eqnarray*}
y (t) = - \frac{1}{2} g t^2 +v_0 t\\
\end{eqnarray*}
となる。
(3)
再び床に達する時刻を$t_1$とすると$y(t_1)=0$となるので
\begin{eqnarray*}
y (t_1) = - \frac{1}{2} g t_1^2 +v_0 t_1 &=&0 \\
\\
(- \frac{1}{2} g t_1 +v_0)\ t_1 &=&0
\end{eqnarray*}
となる。$t_1 \ne 0$より
\begin{eqnarray*}
- \frac{1}{2} g t_1 +v_0 &=&0 \\
\\
t_1 &=& \frac{2v_0}{g}
\end{eqnarray*}
となる。このとき、位置$x$は
\begin{eqnarray*}
x (t_1) &=& - \frac{1}{2} \alpha t_1^2\\
\\
&=& - \frac{1}{2} \alpha \biggl(\frac{2v_0}{g}\biggr)^2\\
\\
&=& - \frac{1}{2} \alpha \frac{4v_0^2}{g^2}\\
\\
&=& - \frac{2\alpha v_0^2}{g^2}
\end{eqnarray*}
となる。
従って戻ったときの位置は
\begin{eqnarray*}
(x,y) =\biggl(-\frac{2\alpha v_0^2}{g^2} ,0 \biggr)
\end{eqnarray*}
となる。