解答
水平面となす角$\theta$の滑らかな斜面に質量$m$の物体を置いた。斜面を左向きに水平加速度$\alpha$で動かしたところ、物体は斜面上で静止していた。以下の問いに答えよ。
(1) 物体の運動方程式を記述せよ。
(2) 斜面の加速度$\alpha$を求めよ。
解答
(1)
動く斜面に固定された座標系において、物体に作用する力は場の力「重力$mg$」と接触力「斜面からの抗力$R$」と慣性力「$m \alpha$」となり、座標軸$x,y$に沿って成分を分解すると図のようになる。(注: 斜面は滑らかで摩擦力が作用しないため、抗力$R$は斜面に垂直な方向にのみ作用し、傾くことはない。)
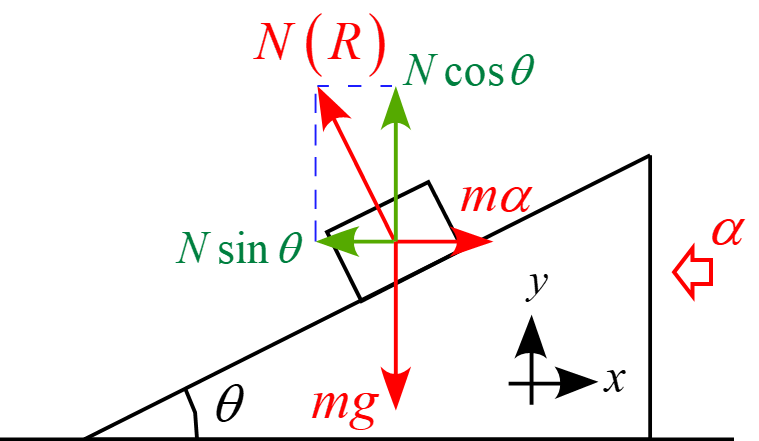
従って、運動方程式は
\begin{eqnarray*}
m a_x &=&m \alpha - N \sin \theta\\
\\
m a_y &=& N\cos \theta -mg
\end{eqnarray*}
物体は斜面上で静止しているので$a_x=0 , a_y=0$
\begin{eqnarray*}
0 &=&m \alpha - N \sin \theta\\
\\
0 &=& N\cos \theta -mg
\end{eqnarray*}
となる。
(2)
$y$軸の運動方程式を変形すると
\begin{eqnarray*}
N\cos \theta &=& mg \\
\\
N &=&\frac{mg}{\cos \theta}
\end{eqnarray*}
となるので、
\begin{eqnarray*}
0 &=&m \alpha - N \sin \theta\\
\\
m \alpha &=& \frac{mg}{\cos \theta}\ \sin \theta\\
\\
\alpha &=& g \tan \theta
\end{eqnarray*}
となる。