問題
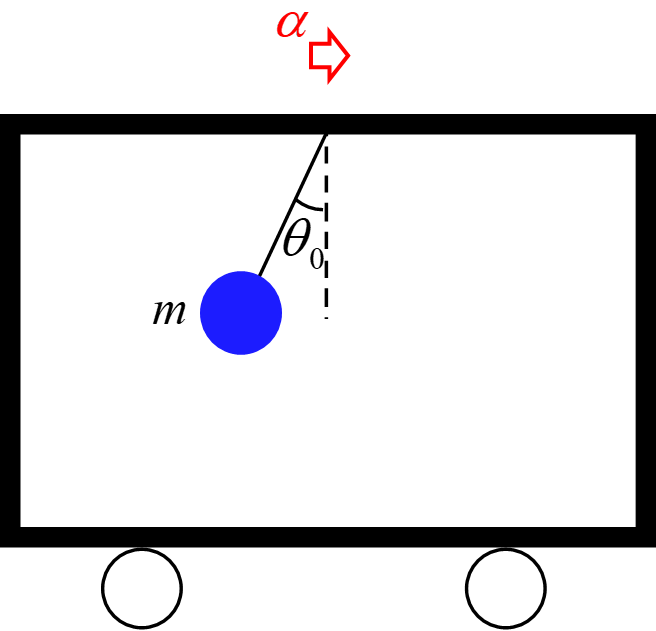
電車が一定の加速度$\alpha$で水平右向きに進んでいる。この電車内で、質量$m$の物体を天井から吊るしたところ、物体は鉛直線となす角度$\theta_0$を保っている。以下の問いに答えよ。
(1) 慣性系における物体の運動方程式を記述せよ。
(2) 車内に固定された座標系における物体の運動方程式を記述せよ。
(3) $\tan \theta_0$を表せ。
(4) 糸の張力$T$を求めよ。
解答
(1)
慣性系において、物体に作用する力は場の力「重力$mg$」と接触力「糸の張力$T$」となり、座標軸$X,Y$に沿って成分を分解すると図のようになる。
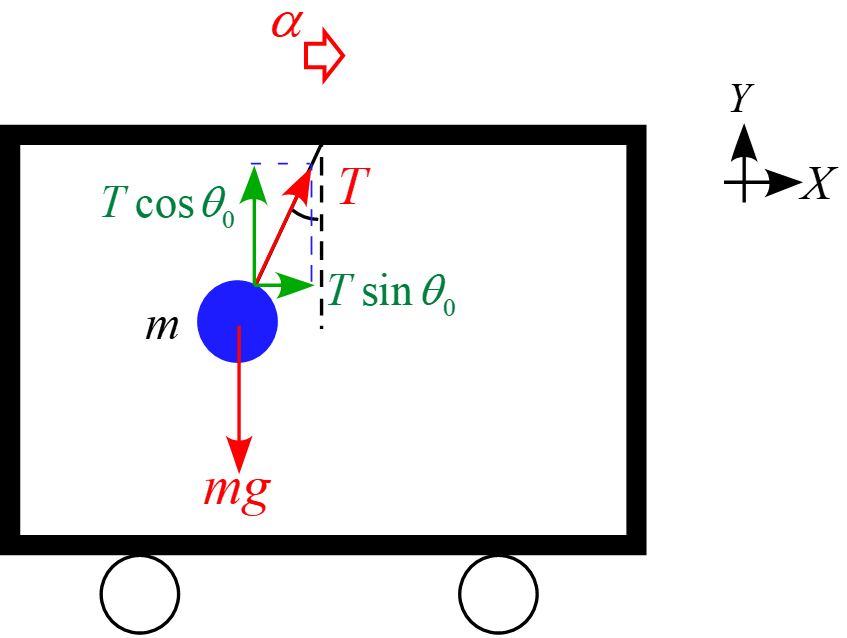
従って、運動方程式は
\begin{eqnarray*}
m a_X &=& T\sin \theta_0 \\
\\
m a_Y &=& T\cos \theta_0 -mg
\end{eqnarray*}
モデルの設定より$a_X=\alpha , a_Y=0$
\begin{eqnarray*}
m \alpha &=& T\sin \theta_0 \\
\\
0 &=& T\cos \theta_0 -mg
\end{eqnarray*}
となる。
(2)
車内に固定された座標系において、物体に作用する力は場の力「重力$mg$」と接触力「糸の張力$T$」と慣性力「$m \alpha$」となり、座標軸$x,y$に沿って成分を分解すると図のようになる。
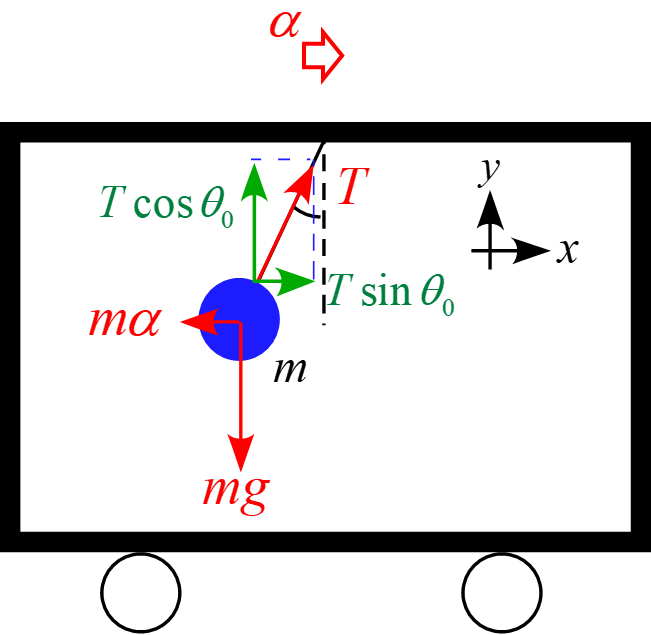
従って、運動方程式は
\begin{eqnarray*}
m a_x &=& T\sin \theta_0 - m \alpha \\
\\
m a_y &=& T\cos \theta_0 -mg
\end{eqnarray*}
鉛直線となす角度$\theta_0$保持より$a_x=0 , a_y=0$
\begin{eqnarray*}
0 &=& T\sin \theta_0 - m \alpha \\
\\
0 &=& T\cos \theta_0 -mg
\end{eqnarray*}
となる。
(3),(4)
(1),(2)の結果はいずれも
\begin{eqnarray*}
T\sin \theta_0 &=& m \alpha \\
\\
T\cos \theta_0 &=& mg
\end{eqnarray*}
と変形できる。
2式の「比」を取ると
\begin{eqnarray*}
\frac{T\sin \theta_0}{T\cos \theta_0} &=& \frac{m \alpha}{mg} \\
\\
\tan \theta_0 &=& \frac{\alpha}{g} \\
\end{eqnarray*}
となる。
2式の「2乗の和」を取ると
\begin{eqnarray*}
(T\sin \theta_0)^2 + (T\cos \theta_0)^2 &=& (m \alpha)^2 + (m g)^2\\
\\
T^2\sin^2 \theta_0 + T^2\cos^2 \theta_0 &=& m^2 \alpha^2 + m^2 g^2\\
\\
T^2(\sin^2 \theta_0 + \cos^2 \theta_0) &=& m^2 (\alpha^2 + g^2)\\
\\
T^2 &=& m^2 (\alpha^2 + g^2)\\
\\
T&=& m \sqrt{\alpha^2 + g^2} \\
\end{eqnarray*}
となる。