問題
摩擦がある斜面を質量$m$の物体が滑り上がる運動を考える。
水平面となす角は$\theta$として以下の問いに答えよ。
但し、動摩擦力は$f=\mu_k N$として用いてよいとする。
斜面に沿って上向きに初速度$v_0$で物体を打ち出したところ、時刻$t_1$で移動距離$L$になり物体は止まった。
(1) この運動中に作用する力を書き込め。
(2) この運動の運動方程式を記述せよ。
(3) 運動方程式の両辺において距離積分を行い、仕事とエネルギーの関係式を導け。
(4) 動摩擦力がした仕事$W_{摩}$を求めよ。
(5) 移動した距離$L$を$v_0, g, \theta, \mu_k$を用いて表せ。

解答
(1)
軸の設定を図の様に設定すると、
運動中に作用する力は、場の力「重力$mg$」と接触力「斜面から受ける抗力$R$」の$2$つあります。(「抗力$R$」は進行方向に対して逆向きに傾きます)
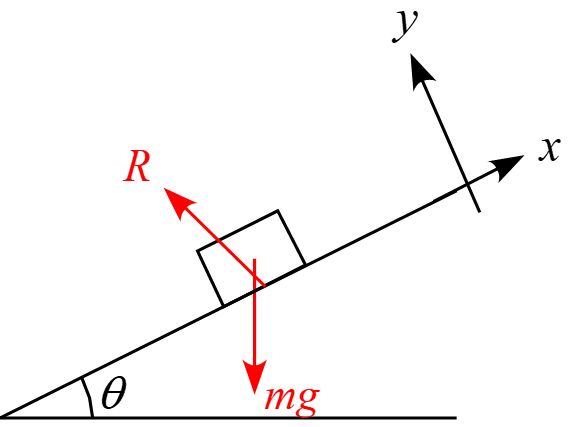
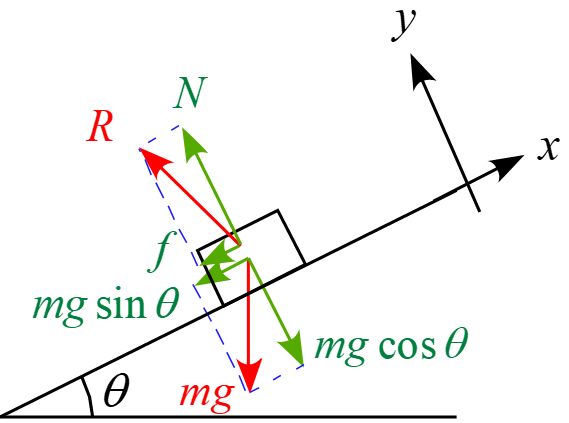
それぞれ軸に対して斜めなので、軸に沿って成分に分解すると、
「重力$mg$」は「$mg \sin \theta , mg \cos \theta$」となり、
「抗力$R$」は「摩擦力$f$, 垂直抗力$N$」となります。
(2)
運動方程式はそれぞれの軸に対しての加速度を$a_x, a_y$とすると
\begin{eqnarray*}
ma_x &=& - mg \sin \theta -f \\
\\
ma_y &=& N - mg \cos \theta\\
\end{eqnarray*}
と表され、斜面に沿った加速度を$a$と表すと、
$a_x=a, \ a_y=0$(束縛条件) , $f=\mu_k N$より
\begin{eqnarray*}
ma &=& - mg \sin \theta -\mu_k N \\
\\
0 &=& N - mg \cos \theta\\
\end{eqnarray*}
より、
\begin{eqnarray*}
ma &=& - mg \sin \theta -\mu_k mg \cos \theta \\
\end{eqnarray*}
となる。
(3)
運動方程式の両辺を$x$で積分すると
\begin{eqnarray*}
m\frac{\diff v}{\diff t} &=& - mg \sin \theta -\mu_k mg \cos \theta \\
\\
\int m\frac{\diff v}{\diff t} \diff x &=& \int (- mg \sin \theta - \mu_k mg \cos \theta)\ \diff x \\
\\
\int m\frac{\diff v}{\diff t} v\ \diff t &=& \int (- mg \sin \theta - \mu_k mg \cos \theta)\ \diff x \\
\\
\int \frac{\diff }{\diff t} \biggl( \frac{1}{2}m v^2 \biggr) \ \diff t&=& \int (- mg \sin \theta - \mu_k mg \cos \theta)\ \diff x \\
\\
\int \frac{\diff }{\diff t} \biggl( \frac{1}{2}m v^2 \biggr) \ \diff t&=& \int (- mg \sin \theta) \diff x + \int (- \mu_k mg \cos \theta)\ \diff x \\
\end{eqnarray*}
となります。この式がこの運動における「仕事とエネルギーの関係式」になります。

積分区間を指定すると
スタート時は
$v(0)=v_0, x(0)=0$、
であり、終点での時刻を$t_1$とすると
$v(t_1)=0, x(t_1)=L$となるので、
\begin{eqnarray*}
\int_0^{t_1} \frac{\diff }{\diff t} \biggl( \frac{1}{2}m v^2 \biggr) \ \diff t&=& \int_{x(0)}^{x(t_1)} (- mg \sin \theta) \diff x + \int_{x(0)}^{x(t_1)} (- \mu_k mg \cos \theta)\ \diff x \\
\\
\biggl[ \frac{1}{2}m v^2 \biggr]_{v_0}^{0} &=& \bigl[- mg \sin \theta \cdot x \bigr]_0^L + \bigl[- \mu_k mg \cos \theta \cdot x \bigr]_0^L \\
\\
\frac{1}{2}m \cdot 0^2 -\frac{1}{2}m v_0^2 &=& - mgL \sin \theta - \mu_k mgL \cos \theta \\
\\
-\frac{1}{2}m v_0^2 &=& - mgL \sin \theta - \mu_k mgL \cos \theta \\
\end{eqnarray*}
となります。
(4)
前式の結果において、
\begin{eqnarray*}
-\frac{1}{2} mv_0^2 &=& -mgL \sin \theta + (- \mu_k mgL \cos \theta)
\end{eqnarray*}
摩擦力による仕事は右辺第2項の部分になるので
\begin{eqnarray*}
W_{摩}= - \mu_k mgL \cos \theta
\end{eqnarray*}

(5)
(3)の結果より
\begin{eqnarray*}
\frac{1}{2} mv_0^2 &=& mg L \sin \theta + \mu_k mg L \cos \theta \\
\\
L &=& \frac{\frac{1}{2} mv_0^2}{mg \sin \theta + \mu_k mg \cos \theta} \\
\\
L &=& \frac{v_0^2}{2g(\sin \theta + \mu_k \cos \theta)}
\end{eqnarray*}
となります。