問題
運動方程式$m \vec{a}=\vec{F}$からモーメントと角運動量の関係式を導け。
但し、位置ベクトルを$\vec{r}=(x, y, z)$として扱うとする。
解答
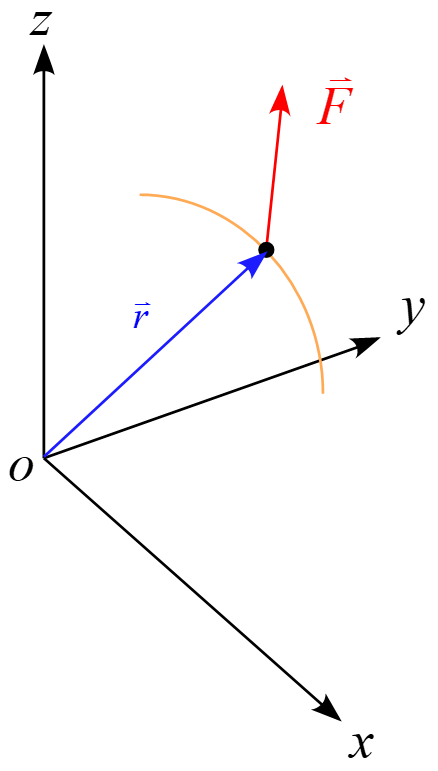
運動方程式$m \vec{a}=\vec{F}$の両辺に左側から位置ベクトル$\vec{r}$の外積をとると、
\begin{eqnarray*}
m \vec{a} &=& \vec{F} \\
\\
m \frac{\diff \vec{v}}{\diff t} &=& \vec{F} \\
\\
\vec{r} \times m \frac{\diff \vec{v}}{\diff t} &=& \vec{r} \times \vec{F} \\
\end{eqnarray*}
と表され、さらに質量$m$を微分の中に入れると
\begin{eqnarray*}
\vec{r} \times \frac{\diff }{\diff t} \bigl( m \vec{v} \bigr)&=& \vec{r} \times \vec{F} \\
\end{eqnarray*}
と表されます。
ここで、左辺の微分の中に位置ベクトルの外積$\vec{r} \times$が入った形
$\displaystyle \frac{\diff }{\diff t} \bigl(\vec{r} \times m \vec{v} \bigr)$に着目し、積の微分で展開すると
\begin{eqnarray*}
\frac{\diff }{\diff t} \bigl(\vec{r} \times m \vec{v} \bigr) &=& \frac{\diff \vec{r}}{\diff t} \times m\vec{v} + \vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\\
&=& \vec{v} \times m\vec{v} + \vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\\
&=& \vec{0} + \vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\\
&=&\vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\end{eqnarray*}
となります。(注)
この形は前式の左辺に等しいので、
\begin{eqnarray*}
\vec{r} \times \frac{\diff }{\diff t} \bigl( m \vec{v} \bigr)&=& \vec{r} \times \vec{F} \\
\\
\frac{\diff }{\diff t} \bigl(\vec{r} \times m \vec{v} \bigr) &=& \vec{r} \times \vec{F}
\end{eqnarray*}
となり、この式が「モーメントと角運動量の関係式」になります。

$\frac{\diff }{\diff t}\bigl(\ \bigr)$の括弧内$\vec{r} \times m \vec{v}$は角運動量$\vec{L}$であり、右辺の$\vec{r} \times \vec{F}$は力のモーメント(トルク)$\vec{M}$になります。
これらを用いて記述し直すと
\begin{eqnarray*}
\frac{\diff \vec{L}}{\diff t} &=& \vec{M}
\end{eqnarray*}
となり、この式を「回転の運動方程式」と呼びます。
注
式変形についてのコメント
\begin{eqnarray*}
\frac{\diff }{\diff t} \bigl(\vec{r} \times m \vec{v} \bigr) &=& \frac{\diff \vec{r}}{\diff t} \times m\vec{v} + \vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\\
&=& \vec{v} \times m\vec{v} + \vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\\
&=& \vec{0} + \vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\\
&=&\vec{r} \times \frac{\diff }{\diff t} \bigl(m \vec{v} \bigr) \\
\end{eqnarray*}
1行目の$\frac{\diff \vec{r}}{\diff t}$は速度$\vec{v}$の定義なので$\vec{v}$と書き換えます。
2行目の$\vec{v} \times m\vec{v}$は自分自身の外積を含んでいるので、なす角$\theta =0$となり$\vec{0}$となります。