問題
図のように、円の一部を軌道として運動するモデルを考える。
物体を糸の水平状態(点A)にして放し、円運動させ、点B(最下点)を通過し、点Cまで達した。運動中、糸は弛まず質量は無視できるほど軽いとする。
糸の長さ$l$、物体の質量$m$として以下の問いに答えよ。但し、重力加速度は$g$とする。
又、ある時刻$t$での糸と鉛直線のなす角を$\theta$として用いてよいとする。

(1) $r$方向、$\theta$方向の加速度を$a_r, a_\theta$としたとき、それぞれの方向の運動方程式を記述せよ。(糸の張力は$T$とする)
(2) 運動方程式に加速度$a_r , a_\theta$を代入し記述せよ。
(3) 極座標表示における$\theta$方向の速度$v_\theta$から $\displaystyle \frac{\diff \theta}{\diff t}, \frac{\diff^2 \theta}{\diff t^2} , \diff \theta$を表せ。($l, v_\theta$を用いて表すこと)
(4) $\theta$方向の運動方程式の両辺を$l \diff \theta$で積分し、ある角$\theta$での仕事とエネルギーの関係式を導け。
(5) 点Bでの仕事とエネルギーの関係式を記述し、速度$v_\text{B}$を求めよ。
(6) $r$方向の運動方程式からある角$\theta$での張力$T$を表せ。($v_\theta$を用いて表すこと)
(7) 点Bでの張力$T_\text{B}$を求めよ。
(8) 点Cでの張力$T_\text{C}$を求めよ。
解答
(1)
運動中、物体に作用する力は「重力$mg$」と「糸の張力$T$」になります。
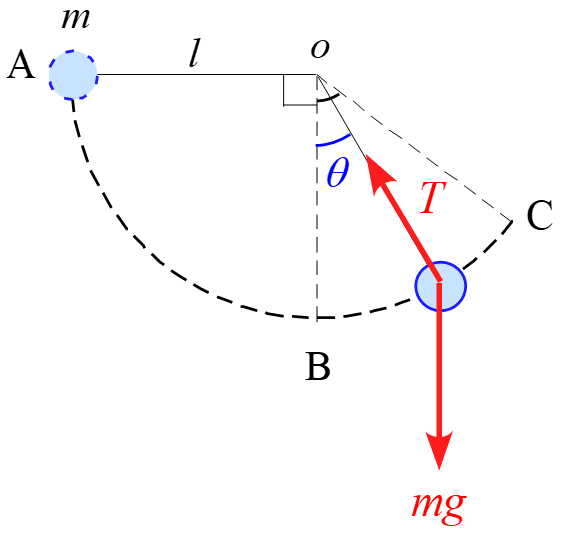
極座標$r , \theta$を設定し、軸に沿って分解すると図のようになります。
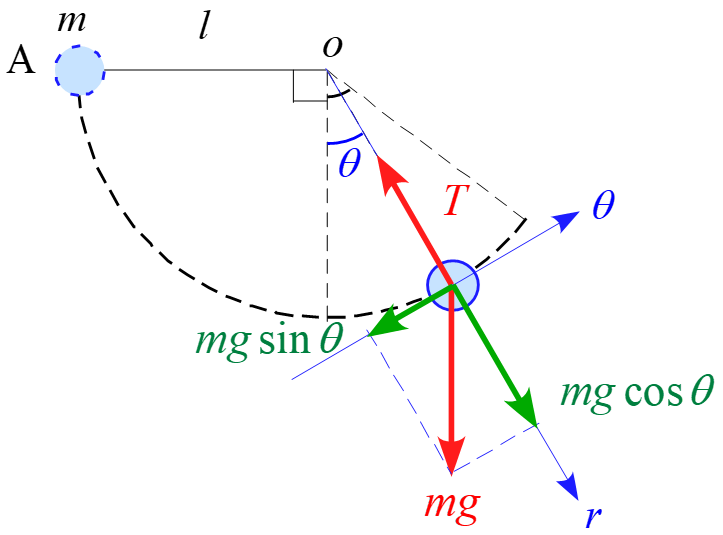
従って、運動方程式は
\begin{eqnarray*}
ma_r &=& mg \cos \theta -T \\
\\
ma_\theta &=& -mg \sin \theta
\end{eqnarray*}
と表されます。
(2)
極座標の加速度$a_r, a_\theta$は一般的に
\begin{eqnarray*}
a_r &=& \frac{\diff^2 r}{\diff t^2} - r\biggl( \frac{\diff \theta}{\diff t}\biggr)^2 \\
\\
a_\theta &=& 2 \frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t} + r \frac{\diff^2 \theta}{\diff t^2}
\end{eqnarray*}
と表されるので、これを代入すると
\begin{eqnarray*}
m \biggl[ \frac{\diff^2 r}{\diff t^2} - r\biggl( \frac{\diff \theta}{\diff t}\biggr)^2 \biggr] &=& mg \cos \theta -T \\
\\
m \biggl[ 2 \frac{\diff r}{\diff t} \frac{\diff \theta}{\diff t} + r \frac{\diff^2 \theta}{\diff t^2} \biggr] &=& -mg \sin \theta
\end{eqnarray*}
となります。
(3)
以降の計算で使用する物理量を下準備として計算する。
極座標の速度$v_\theta$は一般的に$\displaystyle v_\theta = r \frac{\diff \theta}{\diff t}$と表されるので、問題の設定より$r=l$を用いると
\begin{eqnarray*}
\frac{\diff \theta}{\diff t} &=& \frac{v_\theta}{l} \\
\\
\diff \theta &=& \frac{v_\theta}{l} \diff t \\
\\
\frac{\diff^2 \theta}{\diff t^2} &=& \frac{\diff}{\diff t} \biggl( \frac{v_\theta}{l} \biggr) = \frac{1}{l} \frac{\diff v_\theta}{\diff t}\\
\end{eqnarray*}
となります。
(4)
(2)の結果において、$r=l$(一定)なので$\displaystyle \frac{\diff r}{\diff t}=0$となるので、運動方程式は
\begin{eqnarray*}
-m l\biggl( \frac{\diff \theta}{\diff t}\biggr)^2 &=& mg \cos \theta -T \\
\\
ml \frac{\diff^2 \theta}{\diff t^2} &=& -mg \sin \theta
\end{eqnarray*}
となります。
偏角方向($\theta$方向)の運動方程式から「仕事とエネルギーの関係式」を導きます。その後、動径方向($r$方向)の運動方程式から張力$T$を求めます。
ここで、運動の経路を考えると、円に沿った軌道となります。
この軌道に沿って線積分することで「仕事とエネルギーの関係式」が導かれます。
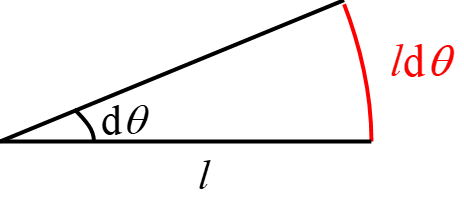
半径$l$の円軌道において、微小角度$\diff \theta$だけ変化した場合の移動距離は$l \diff \theta$なので、偏角方向($\theta$方向)の運動方程式の両辺を変位$l \diff \theta$で積分すると
\begin{eqnarray*}
ml \frac{\diff^2 \theta}{\diff t^2} &=& -mg \sin \theta \\
\\
\int ml \frac{\diff^2 \theta}{\diff t^2} l \diff \theta &=& \int (-mg \sin \theta )\ l \diff \theta \\
\\
\int ml \frac{1}{l} \frac{\diff v_\theta}{\diff t} l \frac{v_\theta}{l} \diff t &=& \int (-mgl \sin \theta ) \diff \theta \\
\\
\int m \frac{\diff v_\theta}{\diff t} v_\theta \diff t &=& \int (-mgl \sin \theta ) \diff \theta \\
\\
\int \frac{\diff}{\diff t} \biggl( \frac{1}{2} m v_\theta^2 \biggr) \diff t &=& \int (-mgl \sin \theta ) \diff \theta
\end{eqnarray*}
となります。
この式がこの運動における「仕事とエネルギーの関係式」になります。

(5)
(4)の結果の「仕事とエネルギーの関係式」に点Aから点Bまでの運動として条件を適用します。
点A : $t=0$ で$\displaystyle \theta(0)= - \frac{\pi}{2} , v_\theta(0)=0$
点B : $t=t_\text{B}$ で$\theta(t_\text{B})=\theta_\text{B}= 0 , v_\theta(t_\text{B})=v_\text{B}$
より
\begin{eqnarray*}
\int_{0}^{t_\text{B}} \frac{\diff}{\diff t} \biggl( \frac{1}{2} m v_\theta^2 \biggr) \diff t &=& \int_{\theta(0)}^{\theta(t_\text{B})} (-mgl \sin \theta ) \diff \theta \\
\\
\biggl[ \frac{1}{2} m v_\theta^2 \biggr]_{0}^{v_\text{B}} &=& mgl \biggl[ \cos \theta \biggr]_{- \frac{\pi}{2}}^{0} \\
\\
\frac{1}{2} m v_\text{B}^2 - \frac{1}{2} m \cdot 0^2 &=& mgl \biggl[ \cos 0 - \cos \biggl( -\frac{\pi}{2} \biggr) \biggr] \\
\\
\frac{1}{2} m v_\text{B}^2 &=& mgl
\end{eqnarray*}
となります。
(この式が、所謂、高校物理で学習する「エネルギー保存則の式」になります。)
従って、点Bでの速度$v_\text{B}$は
\begin{eqnarray*}
v_\text{B}^2 &=& 2gl \\
\\
v_\text{B} &=& \sqrt{2gl} \\
\end{eqnarray*}
となります。
(6)
動径方向の運動方程式を用いて$T$を表すと
\begin{eqnarray*}
-m l\biggl( \frac{\diff \theta}{\diff t}\biggr)^2 &=& mg \cos \theta -T \\
\\
T &=& mg \cos \theta + m l\biggl( \frac{\diff \theta}{\diff t}\biggr)^2 \\
\\
&=& mg \cos \theta + m l\biggl( \frac{v_\theta}{l}\biggr)^2 \\
\\
&=& mg \cos \theta + m \frac{v_\theta^2}{l}
\end{eqnarray*}
となります。
(7)
点Bでの条件$\theta(t_\text{B})=\theta_\text{B}= 0 , v_\theta(t_\text{B})=v_\text{B}$を代入すると
\begin{eqnarray*}
T_\text{B}&=& mg \cos \theta_\text{B}+ m \frac{v_\text{B}^2}{l} \\
\\
&=& mg \cos 0 + m \frac{2gl}{l} \\
\\
&=& mg + 2mg \\
\\
&=& 3mg
\end{eqnarray*}
となります。
(8)
点Bの場合と同様に、(4)の結果の「仕事とエネルギーの関係式」に点Aから点Cまでの運動として条件を適用します。
点A : $t=0$ で$\displaystyle \theta(0)= - \frac{\pi}{2} , v_\theta(0)=0$
点C : $t=t_\text{C}$ で$\theta(t_\text{C})= \theta_\text{C} , v_\theta(t_\text{C})=v_\text{C}$
より
\begin{eqnarray*}
\int_{0}^{t_\text{C}} \frac{\diff}{\diff t} \biggl( \frac{1}{2} m v_\theta^2 \biggr) \diff t &=& \int_{\theta(0)}^{\theta(t_\text{C})} (-mgl \sin \theta ) \diff \theta \\
\\
\biggl[ \frac{1}{2} m v_\theta^2 \biggr]_{0}^{v_\text{C}} &=& mgl \biggl[ \cos \theta \biggr]_{- \frac{\pi}{2}}^{\theta_\text{C}} \\
\\
\frac{1}{2} m v_\text{C}^2 - \frac{1}{2} m \cdot 0^2 &=& mgl \biggl[ \cos \theta_\text{C} - \cos \biggl( -\frac{\pi}{2} \biggr) \biggr] \\
\\
\frac{1}{2} m v_\text{C}^2 &=& mgl \cos \theta_\text{C}
\end{eqnarray*}
となります。
従って、点Cでの速度$v_\text{C}$は
\begin{eqnarray*}
v_\text{C}^2 &=& 2gl \cos \theta_\text{C}\\
\\
v_\text{C} &=& \sqrt{2gl \cos \theta_\text{C}} \\
\end{eqnarray*}
となります。
動径方向の運動方程式については
点Cでの条件$\theta(t_\text{C})=\theta_\text{C} , v_\theta(t_\text{C})=v_\text{C}$を代入すると
\begin{eqnarray*}
T_\text{C}&=& mg \cos \theta_\text{C}+ m \frac{v_\text{C}^2}{l} \\
\\
&=& mg \cos \theta_\text{C} + m \frac{2gl \cos \theta_\text{C}}{l} \\
\\
&=& mg\cos \theta_\text{C} + 2mg \cos \theta_\text{C} \\
\\
&=& 3mg\cos \theta_\text{C}
\end{eqnarray*}
となります。