問題
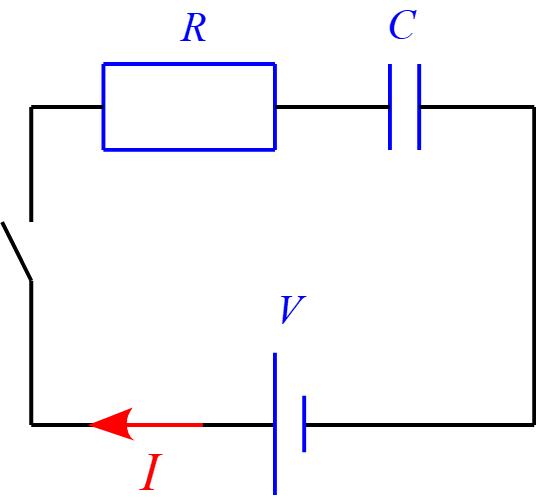
図のようなRC回路を考える。スイッチを入れる前にコンデンサーに電荷は蓄えられていないものとする。時刻$t=0$でスイッチを入れたとして以下の問いに答えよ。
(1) この回路の回路方程式を記述せよ。ある時刻$t$におけるコンデンサーの電荷を$Q(t)$としてよい。
(2) 時計回りの向きを正として、$t=0$における電流$I(0)$を求めよ。
(3) 十分に時間が経った後のコンデンサーの電荷$Q(\infty)$を求めよ。
(4) $Q-t$グラフを描け。また、$Q-t$グラフの原点での傾きを求めよ。
(5) この回路におけるエネルギーの関係式を導け。
解答
(1)
キルヒホッフの法則より回路方程式は
\begin{eqnarray*}
RI(t)+\frac{Q(t)}{C} = V
\end{eqnarray*}
と表される。
(2)
$t=0$において回路方程式は
\begin{eqnarray*}
RI(0)+\frac{Q(0)}{C} = V
\end{eqnarray*}
と表され、初期条件$Q(0)=0$より
\begin{eqnarray*}
RI(0)+\frac{0}{C} &=& V \\
\\
RI(0) &=& V \\
\\
I(0) &=& \frac{V}{R}
\end{eqnarray*}
となる。
(3)
電流の定義$\displaystyle I=\frac{\diff Q}{\diff t}$を回路方程式に代入すると
\begin{eqnarray*}
R\frac{\diff Q(t)}{\diff t}+\frac{Q(t)}{C} = V
\end{eqnarray*}
となり、$Q$に関する微分方程式として記述される。
従って
\begin{eqnarray*}
R\frac{\diff Q(t)}{\diff t}+\frac{Q(t)}{C} &=& V \\
\\
R\frac{\diff Q(t)}{\diff t} &=& V - \frac{Q(t)}{C}\\
\\
\frac{\diff Q(t)}{\diff t} &=& \frac{V}{R}- \frac{Q(t)}{RC}\\
\\
\frac{\diff Q(t)}{\diff t} &=& \frac{CV-Q(t)}{RC} \\
\\
\frac{\diff Q(t)}{CV-Q(t)} &=& \frac{ \diff t }{RC}\\
\\
\int \frac{\diff Q(t)}{CV-Q(t)} &=& \int \frac{ \diff t }{RC}\\
\\
- \log(CV-Q(t)) &=& \frac{1}{RC} t +C_1 \qquad (C_1: \mbox{積分定数}) \\
\\
\\
\log(CV-Q(t)) &=& -\frac{1}{RC} t -C_1 \\
\\
CV-Q(t) &=& e^{-\frac{1}{RC} t -C_1} \\
\\
CV-Q(t) &=& e^{-C_1} \cdot e^{-\frac{1}{RC} t}\\
\\
Q(t) &=& CV - e^{-C_1} \cdot e^{-\frac{1}{RC} t} \\
\\
Q(t) &=& CV - C_2 \cdot e^{-\frac{1}{RC} t} \qquad (C_2=e^{-C_1})\\
\end{eqnarray*}
となる。ここで初期条件$Q(0)=0$より
\begin{eqnarray*}
Q(0) = CV - C_2 \cdot e^{-\frac{1}{RC}\cdot 0} &=& 0 \\
\\
CV -C_2 &=& 0 \\
\\
C_2 &=& CV
\end{eqnarray*}
従って
\begin{eqnarray*}
Q(t) &=& CV - CV \cdot e^{-\frac{1}{RC}t} \\
\\
&=& CV(1-e^{-\frac{1}{RC}t})
\end{eqnarray*}
となる。
十分に時間が経ったとき、即ち$t=\infty$の時
\begin{eqnarray*}
Q(t) &=& CV(1-e^{-\frac{1}{RC}\infty}) \\
&=& CV
\end{eqnarray*}
となる。
電流$I$は
\begin{eqnarray*}
I = \frac{\diff Q(t)}{\diff t} &=& \frac{\diff}{\diff t} \biggl[ CV(1-e^{-\frac{1}{RC}t}) \biggr]
\\
&=& CV (- e^{-\frac{1}{RC}t})\cdot -\frac{1}{RC} \\
\\
&=& \frac{V}{R} e^{-\frac{1}{RC}t}
\end{eqnarray*}
となる。$t=0$を代入すると
\begin{eqnarray*}
I(0) &=& \frac{V}{R} e^{-\frac{1}{RC} \cdot 0} =\frac{V}{R}
\end{eqnarray*}
となり、また$t=\infty$を代入すると
\begin{eqnarray*}
I(\infty) = \frac{V}{R} e^{-\frac{1}{RC} \infty } = 0
\end{eqnarray*}
となるので、前問の結果と一致する。
これらを合わせてグラフを描くと下図のようになる。
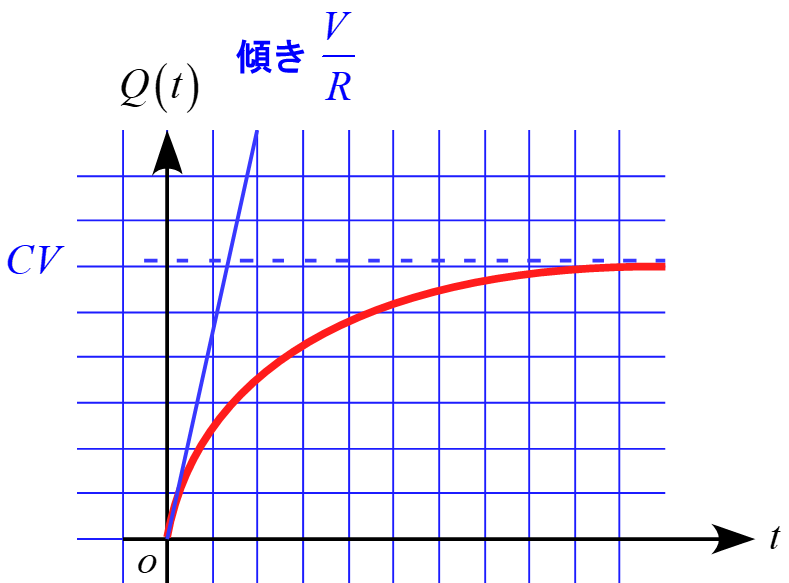
(5)
回路方程式の両辺に電流$\displaystyle I=\frac{\diff Q}{\diff t}$をかけると
\begin{eqnarray*}
RI+\frac{Q}{C} & = & V \\
\\
RI^2+\frac{Q}{C}\frac{\diff Q}{\diff t} & = & V\frac{\diff Q}{\diff t} \\
\\
RI^2+\frac{\diff}{\diff t} \biggl(\frac{1}{2} \frac{Q^2}{C} \biggr)& = & V\frac{\diff Q}{\diff t}
\end{eqnarray*}
となる。
左辺第1項は「抵抗で単位時間に消費されるジュール熱」、左辺第2項は「コンデンサーのエネルギーの時間変化量」、右辺は「単位時間に電源がする仕事(仕事率)」を表している。