問題
半径 $a$ の無限に長い円筒に定常電流 $i$ が流れているとする。以下の問いに答えよ。ただし、円筒の中心軸を $z$ 軸とする。
(1) 円筒の外側、中心軸からの距離 $r$ が $r > a$ の位置での磁場 $B$ を求めよ。
(2) 円筒の内側、中心軸からの距離 $r$ が $r < a$ の位置での磁場 $B$ を求めよ。
(3) 磁場 $B(r)$ のグラフを描け。

解答
アンペールの法則
\begin{eqnarray*}
\oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\
\\
\mbox{閉曲面$S$の縁$C$に沿っての磁場の線積分} &=& \mu_0 \times \mbox{閉曲面$S$を貫く電気量}
\end{eqnarray*}
(1)
閉曲面を図のような半径$r\ (>a)$の円とすると
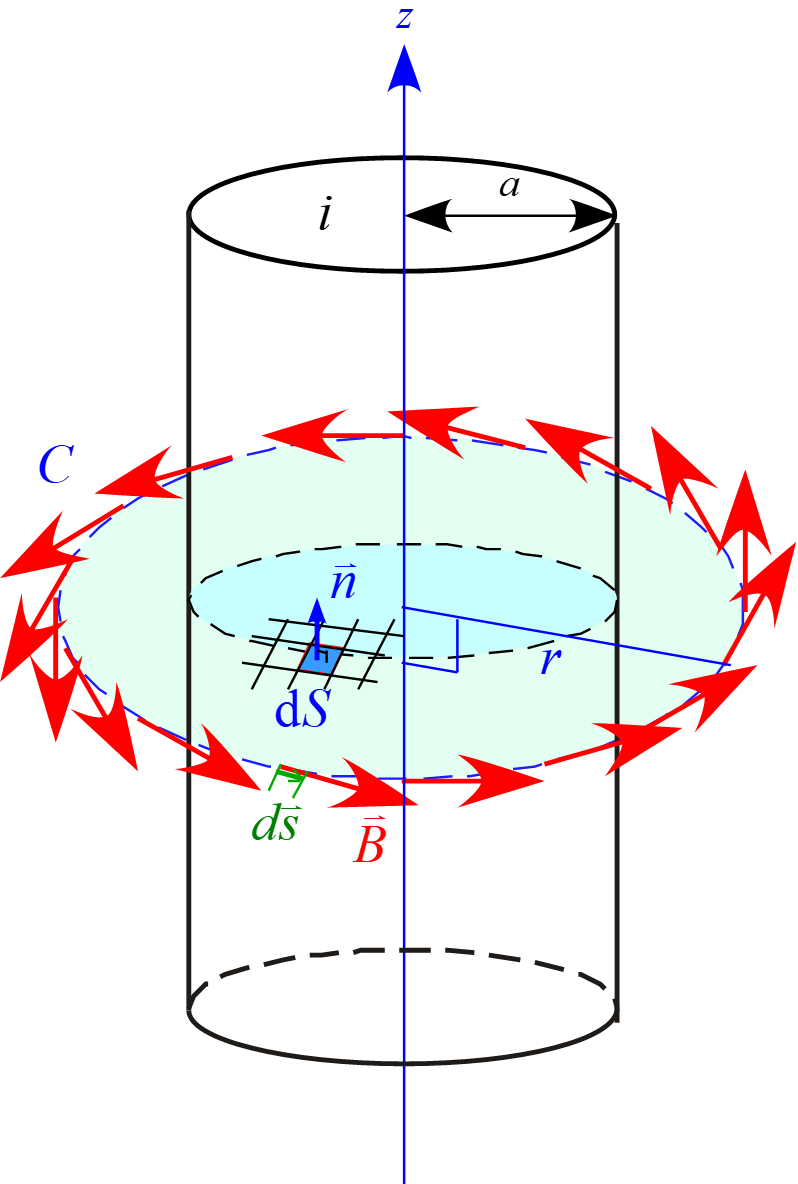
閉曲面$S$の縁$C$に沿っての磁場の線積分については
\begin{eqnarray*}
\oint_C \vec{B} \cdot \diff \vec{s} &=& \int_0^{2\pi R} |\vec{B}|\ |\diff \vec{s}| cos 0 \qquad (\vec{B} \parallel \diff \vec{s})\\
\\
&=& B\int_0^{2\pi R} \diff s \\
\\
&=& B\cdot 2\pi R
\end{eqnarray*}
となる。
また、閉曲面$S$を貫く電気量については
\begin{eqnarray*}
\int_S \vec{i} \cdot \diff\vec{S} &=& \int_S \vec{i}\cdot \vec{n} \diff S\\
\\
&=& \int_S |\vec{i}|\ |\vec{n}| \cos 0 \diff S \qquad (\vec{i} \parallel \vec{n})\\
\\
&=& \int_S i \diff S \\
\\
&=& i
\end{eqnarray*}
となる。
従って、
\begin{eqnarray*}
\oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\
\\
B \cdot 2\pi R &=& \mu_0 I\\
\\
B &=& \frac{\mu_0 i}{2 \pi}\frac{1}{r}
\end{eqnarray*}
となる。
(2)
閉曲面を図のような半径$r\ (< a)$の円とすると
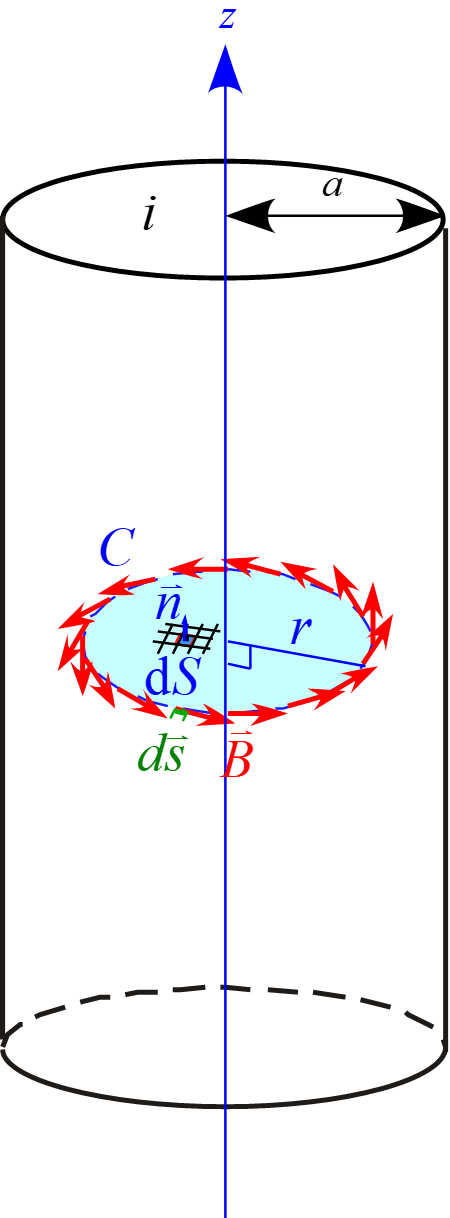
閉曲面$S$の縁$C$に沿っての磁場の線積分については
\begin{eqnarray*}
\oint_C \vec{B} \cdot \diff \vec{s} &=& \int_0^{2\pi R} |\vec{B}|\ |\diff \vec{s}| cos 0 \qquad (\vec{B} \parallel \diff \vec{s})\\
\\
&=& B\int_0^{2\pi R} \diff s \\
\\
&=& B\cdot 2\pi R
\end{eqnarray*}
となる。
また、閉曲面$S$を貫く電気量については電流$i$が一様な定常電流であるため
閉曲面内部を貫く電流を$i_{in}$とすると
\begin{eqnarray*}
\pi a^2 : \pi r^2 &=& i : i_{in} \\
\\
i_{in} \pi a^2 &=& i \pi r^2 \\
\\
i_{in} &=& \frac{r^2}{a^2}i
\end{eqnarray*}
が成立する。
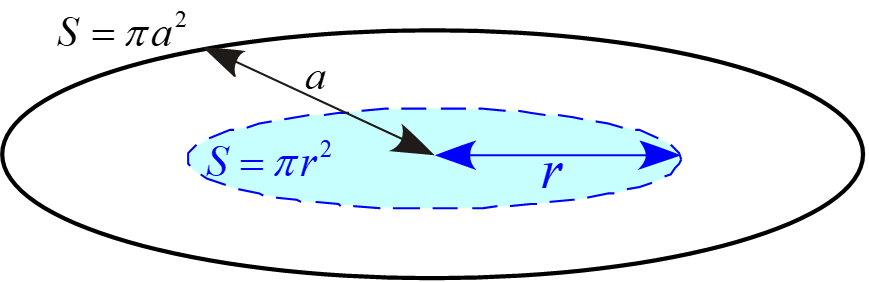
よって
\begin{eqnarray*}
\int_S \vec{i} \cdot \diff\vec{S} &=& \int_S \vec{i}\cdot \vec{n} \diff S\\
\\
&=& \int_S |\vec{i}|\ |\vec{n}| \cos 0 \diff S \qquad (\vec{i} \parallel \vec{n})\\
\\
&=& \int_S i \diff S \\
\\
&=& \frac{r^2}{a^2}i
\end{eqnarray*}
となる。
従って、
\begin{eqnarray*}
\oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\
\\
B \cdot 2\pi r &=& \mu_0 \frac{r^2}{a^2}i\\
\\
B &=& \frac{\mu_0 i}{2 \pi a^2} r
\end{eqnarray*}
となる。
(3)
(1),(2)の結果より
\begin{eqnarray*}
B (r) &=& \frac{\mu_0 i}{2 \pi a^2} r \qquad (r \le a)\\
\\
B (r) &=& \frac{\mu_0 i}{2 \pi}\frac{1}{r} \qquad \ (r \ge a)\\
\end{eqnarray*}
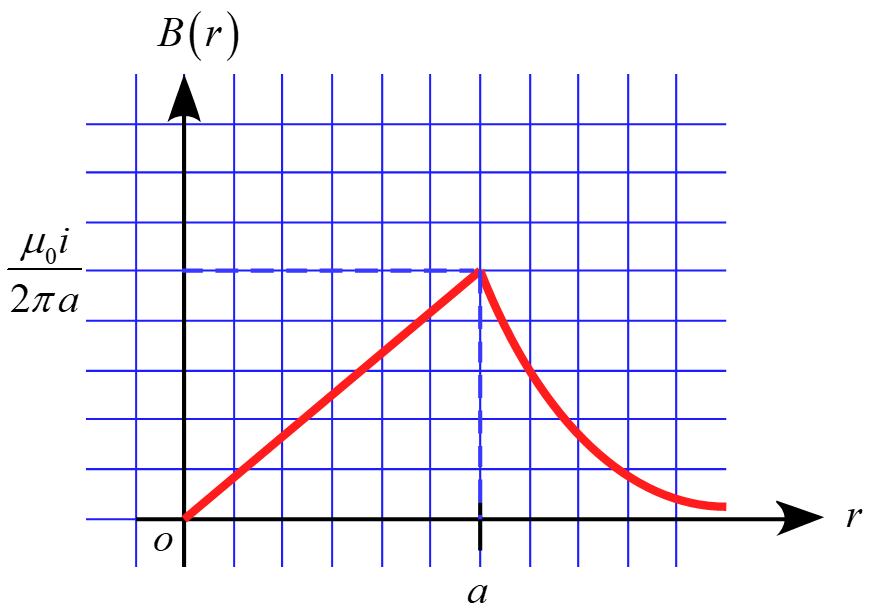
となる。