直線電流が作る磁場 ~ アンペールの法則

問題

無限に長い直線電流$\vec{I}$が作る磁場を求めよ。

解答

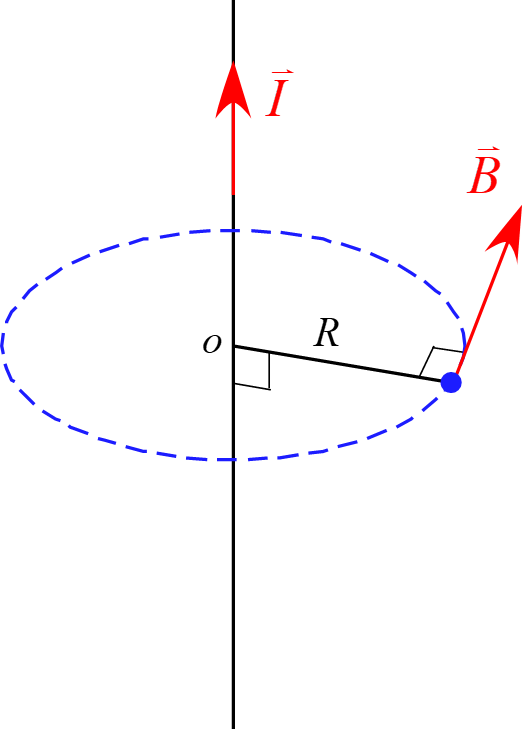
アンペールの法則を適用する閉曲面$S$を電流$\vec{I}$が中心を通る半径$R$の円に設定すると

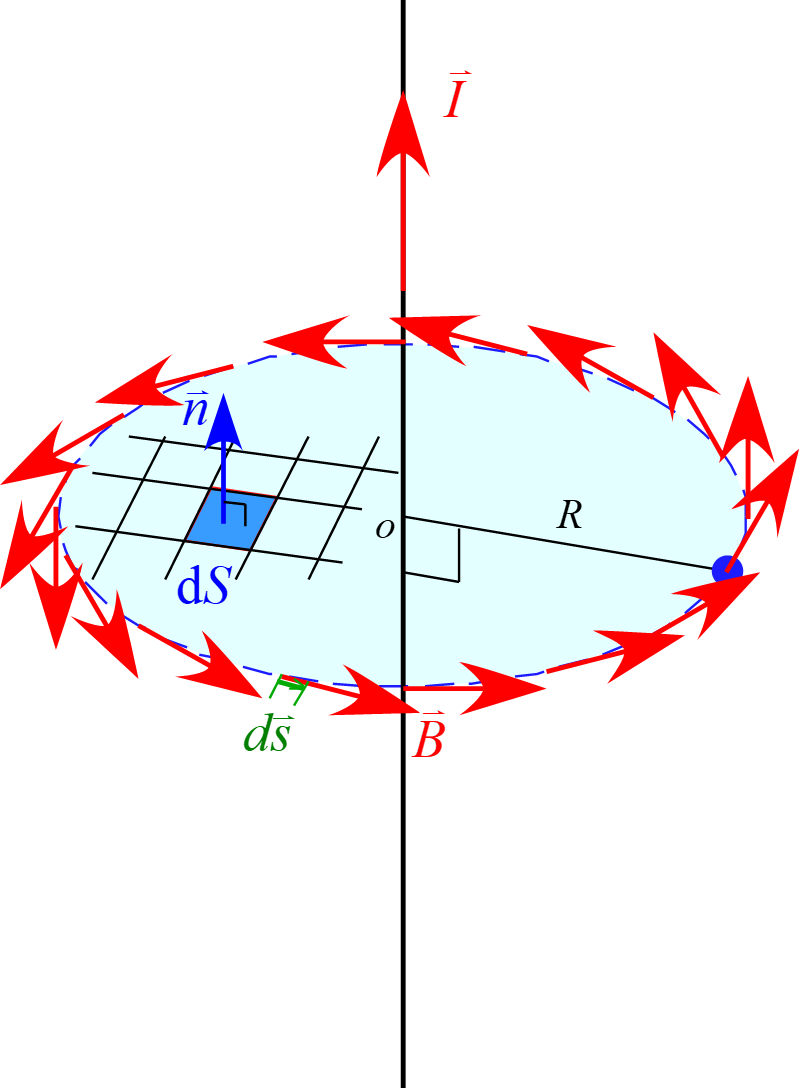
アンペールの法則

$$\begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\ \\ \mbox{閉曲面$S$の縁$C$に沿っての磁場の線積分} &=& \mu_0 \times \mbox{閉曲面$S$を貫く電気量} \end{eqnarray*}$$
より、閉曲面$S$の縁$C$に沿っての磁場の線積分については
$$\begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \int_0^{2\pi R} |\vec{B}|\ |\diff \vec{s}| cos 0 \qquad (\vec{B} \parallel \diff \vec{s})\\ \\ &=& B\int_0^{2\pi R} \diff s \\ \\ &=& B\cdot 2\pi R \end{eqnarray*}$$

また、閉曲面$S$を貫く電気量については

$$\begin{eqnarray*} \int_S \vec{i} \cdot \diff\vec{S} &=& \int_S \vec{i}\cdot \vec{n} \diff S\\ \\ &=& \int_S |\vec{i}|\ |\vec{n}| \cos 0 \diff S \qquad (\vec{i} \parallel \vec{n})\\ \\ &=& \int_S i \diff S \\ \\ &=& I \end{eqnarray*}$$
となる。

従って、

$$\begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\ \\ B \cdot 2\pi R &=& \mu_0 I\\ \\ B &=& \frac{\mu_0 I}{2 \pi R} \end{eqnarray*}$$
となる。

この式を見ると

$$\begin{eqnarray*} B &=& \frac{\mu_0}{2 \pi} \cdot \frac{I}{R} \end{eqnarray*}$$
であるから、電流$I$に比例し、電流からの距離$R$に反比例する量であることが解るので、磁場$B$を$r$の関数と見なし
$$\begin{eqnarray*} B (r) &=& \frac{\mu_0 I}{2 \pi} \cdot \frac{1}{r} \end{eqnarray*}$$
と表すこともできる。