問題
$z$軸方向に一様な磁場$\vec{B}$がある。この磁場内で運動する荷電粒子について論ぜよ。但し、荷電粒子の質量$m$、電荷を$q$とする。
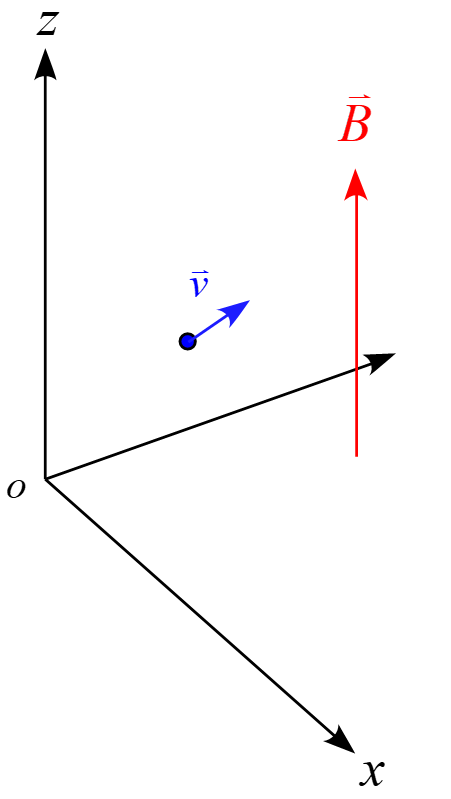
解答
一様な磁場内$\vec{B}$で運動する荷電粒子に作用する力はローレンツ力が作用するので運動方程式は
\begin{eqnarray*}
m \frac{\diff \vec{v}}{\diff t} = q(\vec{v} \times \vec{B})
\end{eqnarray*}
と表される。
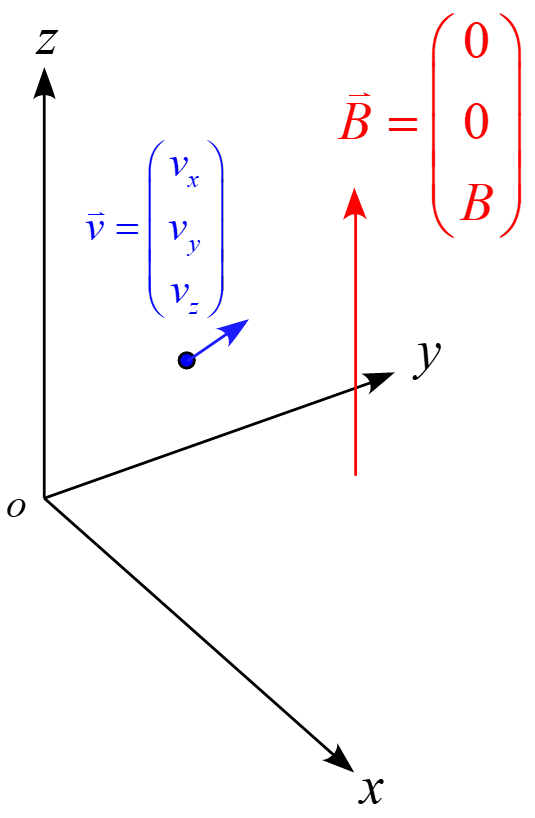
成分で表すと
\begin{eqnarray*}
m
\left(
\begin{array}{c}
\frac{\diff v_x}{\diff t} \\\\
\frac{\diff v_y}{\diff t} \\\\
\frac{\diff v_z}{\diff t}
\end{array}
\right) &=& q
\left(
\begin{array}{c}
v_x \\
v_y \\
v_z
\end{array}
\right) \times
\left(
\begin{array}{c}
0 \\
0 \\
B
\end{array}
\right) \\
\\
&=& q
\left(
\begin{array}{c}
v_y \cdot B - v_z \cdot 0\\
v_x \cdot 0 - v_x \cdot B\\
v_x \cdot 0 - v_y \cdot 0
\end{array}
\right) \\
\\
&=& q
\left(
\begin{array}{c}
v_yB \\
-v_xB \\
o
\end{array}
\right)
\end{eqnarray*}
となる。
従って、それぞれの加速度は
\begin{eqnarray*}
\frac{\diff v_x}{\diff t} &=& \frac{qB}{m} v_y \\
\\
\frac{\diff v_y}{\diff t} &=& -\frac{qB}{m} v_x \\
\\
\frac{\diff v_z}{\diff t} &=& 0 \\
\end{eqnarray*}
となり、連立微分方程式で表される。
$x$成分の式を$t$で微分すると
\begin{eqnarray*}
\frac{\diff v_x}{\diff t} &=& \frac{qB}{m} v_y \\
\\
\frac{\diff}{\diff t}\biggl(\frac{\diff v_x}{\diff t}\biggr) &=& \frac{\diff}{\diff t}\biggl(\frac{qB}{m} v_y \biggr)\\
\\
\frac{\diff^2 v_x}{\diff t^2} &=& \frac{qB}{m} \frac{\diff v_y}{\diff t} = \frac{qB}{m} \cdot -\frac{qB}{m} v_x \\
\\
&=& - \biggl( \frac{qB}{m} \biggr)^2 v_x
\end{eqnarray*}
となる。ここで$\omega = \frac{qB}{m}$と置くと
\begin{eqnarray*}
\frac{\diff^2 v_x}{\diff t^2} = - \omega^2 v_x
\end{eqnarray*}
となる。
この微分方程式の一般解は
\begin{eqnarray*}
v_x(t) = \alpha \cos \omega t + \beta \cos \omega t \qquad (\alpha , \beta :\mbox{任意定数})\\
\end{eqnarray*}
となる。
$v_y$については$x$成分の式より
\begin{eqnarray*}
\frac{\diff v_x}{\diff t} &=& \omega v_y \\
\\
v_y &=& \frac{1}{\omega} \frac{\diff v_x}{\diff t} \\
\\
&=& \frac{1}{\omega} \frac{\diff}{\diff t} (\alpha \cos \omega t + \beta \cos \omega t) \\
\\
&=& \frac{1}{\omega} [\alpha (-\sin \omega t) \cdot \omega +\beta \cos \omega t \cdot \omega ] \\
\\
&=& -\alpha \sin \omega t + \beta \cos \omega t
\end{eqnarray*}
となる。
従って、速度$v_x(t), v_y(t)$は
\begin{eqnarray*}
v_x(t) &=& \alpha \cos \omega t + \beta \cos \omega t \\
\\
v_y(t) &=& -\alpha \sin \omega t + \beta \cos \omega t
\end{eqnarray*}
となる。
それぞれから$x(t) ,y(t)$を求めると
\begin{eqnarray*}
v_x(t) = \frac{\diff x(t)}{\diff t} &=& \alpha \cos \omega t + \beta \cos \omega t \\
\\
\int \frac{\diff x(t)}{\diff t} \diff t &=& \int (\alpha \cos \omega t + \beta \cos \omega t) \diff t \\
\\
\int \diff x(t) &=& \int (\alpha \cos \omega t + \beta \cos \omega t) \diff t \\
\\
x(t) &=& \frac{1}{\omega}\alpha \sin \omega t
+ \frac{1}{\omega} \beta (-\sin \omega t) +C_1 \qquad (C_1:\mbox{積分定数})\\
\\
&=& \frac{\alpha}{\omega} \sin \omega t - \frac{\beta}{\omega} \cos \omega t +C_1 \\
\end{eqnarray*}
続いて
\begin{eqnarray*}
v_y(t) = \frac{\diff y(t)}{\diff t} &=& -\alpha \sin \omega t + \beta \cos \omega t \\
\\
\int \frac{\diff y(t)}{\diff t} \diff t &=& \int ( -\alpha \sin \omega t + \beta \cos \omega t ) \diff t \\
\\
\int \diff y(t) &=& \int ( -\alpha \sin \omega t + \beta \cos \omega t ) \diff t \\
\\
y(t) &=& - \frac{1}{\omega} \alpha (-\cos \omega t) + \frac{1}{\omega} \beta \sin \omega t + C_2 \qquad (C_1:\mbox{積分定数})\\
\\
&=& \frac{\alpha}{\omega} \cos \omega t + \frac{\beta}{\omega} \sin \omega t + C_2
\end{eqnarray*}
となる。
ここで$\displaystyle R\cos \theta = -\frac{b}{\omega}, R\sin \theta = \frac{\alpha}{\omega}$となるように$R$と$\omega$を設定すると
\begin{eqnarray*}
x(t) &=& \frac{\alpha}{\omega} \sin \omega t - \frac{\beta}{\omega} \cos \omega t +C_1 \\
\\
&=& R \sin \theta \sin \omega t + R \cos \theta \cos \omega t +C_1 \\
\\
&=& R \cos (\theta - \omega t) +C_1 \\
\\
y(t)&=& \frac{\alpha}{\omega} \cos \omega t + \frac{\beta}{\omega} \sin \omega t + C_2 \\
\\
&=& R \sin \theta \cos \omega t - R \cos \theta \sin \omega t + C_2 \\
\\
&=& R \sin (\theta - \omega t) + C_2
\end{eqnarray*}
となる。
$z$軸については
\begin{eqnarray*}
\frac{\diff v_z}{\diff t} &=& 0 \\
\\
\int \frac{\diff v_z}{\diff t} \diff t &=& \int 0 \diff t \\
\\
\int \diff v_z &=& \int 0 \diff t \\
\\
v_z &=& C_3 =\mbox{const.} \qquad (C_3:\mbox{積分定数}) \\
\\
\frac{\diff z(t)}{\diff t} &=& v_z \\
\\
\int \frac{\diff z(t)}{\diff t} \diff t &=& \int v_z \diff t \\
\\
\int \diff z(t) &=& \int v_z \diff t \\
\\
z(t) &=& v_z t +C_4 \qquad (C_4:\mbox{積分定数}) \\
\end{eqnarray*}
となる。$t=0$で$z(0)=Z_0$とすると
\begin{eqnarray*}
z(0) = v_z \cdot 0 +C_4 &=& z_0 \\
\\
C_4 &=& z_0
\end{eqnarray*}
となるので
\begin{eqnarray*}
z(t) = v_z t + z_0 \\
\end{eqnarray*}
となる。
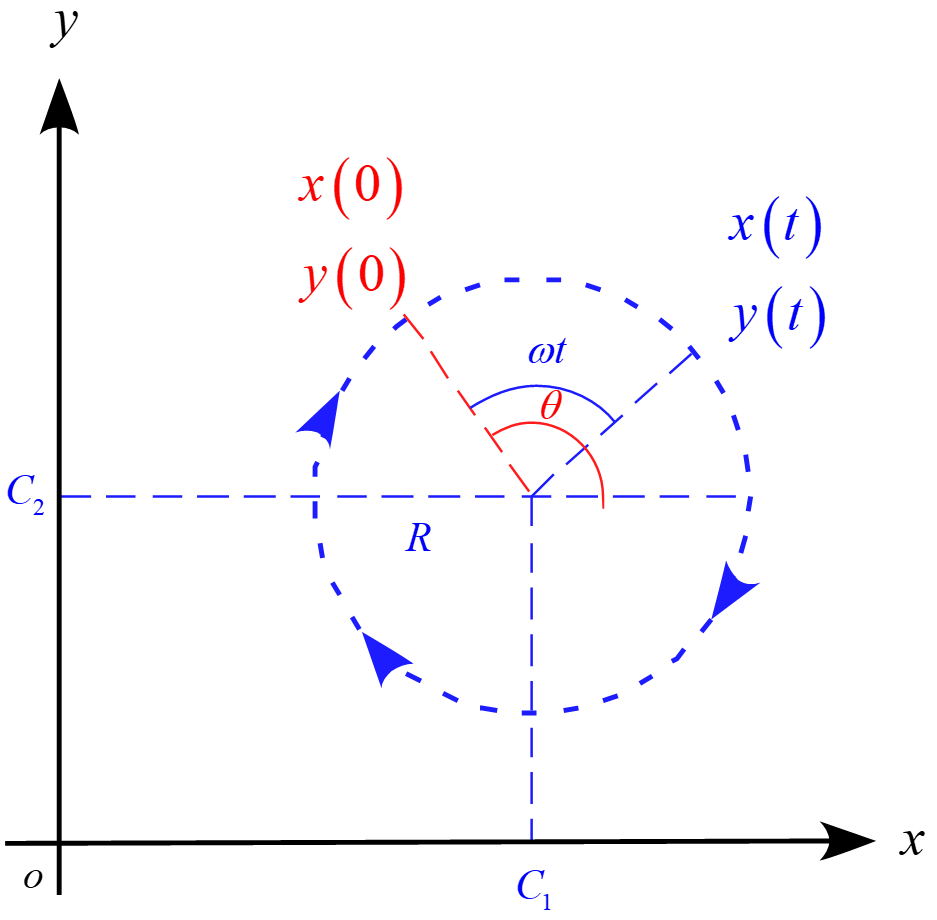
以上より、結果をまとめると
\begin{eqnarray*}
x(t) &=& R \cos (\theta - \omega t) +C_1 \\
\\
y(t) &=& R \sin (\theta - \omega t) + C_2 \\
\\
z(t) &=& v_z t + z_0 \\
\end{eqnarray*}
$x-y$平面では回転運動、$z$軸方向は等速度運動になり、これらをあわせると螺旋運動になります。
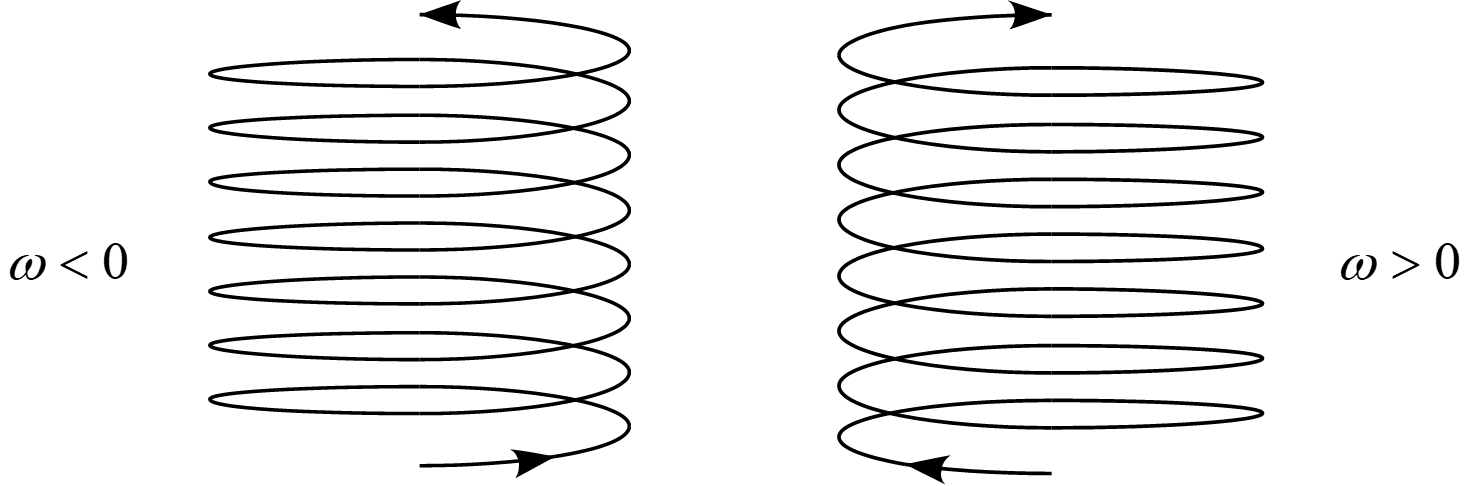
$\omega <0$の時、円運動は反時計回りになり、$\omega >0$の時、円運動は時計回りになります。