問題
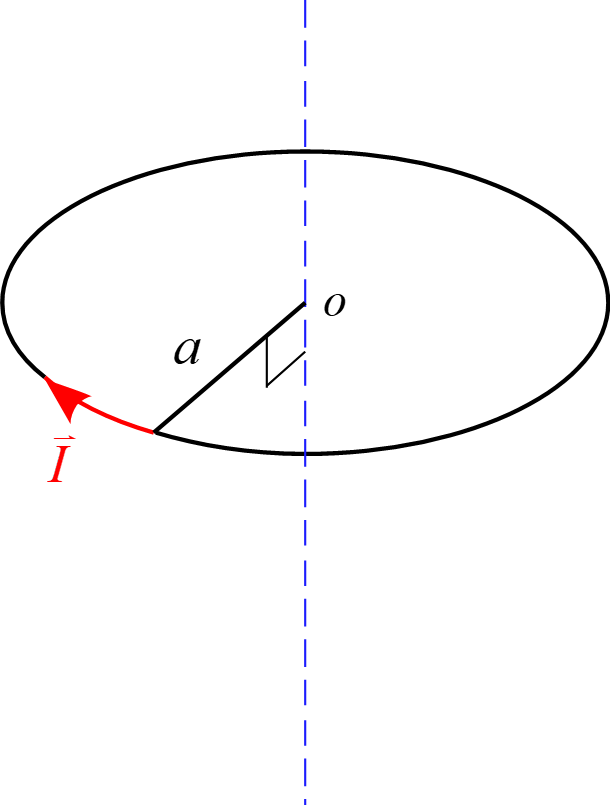
半径$a$の円形電流に時計回りの電流$\vec{I}$が流れている。
この円形電流が作る磁場について以下の問いに答えよ。
(1) 半径$a$の円形電流が中心軸上に作る磁場$B_z$を求めよ。
(2) 半径$a$の円形電流が中心点$o$に作る磁場$B_{z_0}$を求めよ。
解答
(1)
円形電流の微小部分$\diff \vec{s}$を設定し、この微小部分が中心軸上の中心から距離$z$離れた位置に作る磁場を考える。
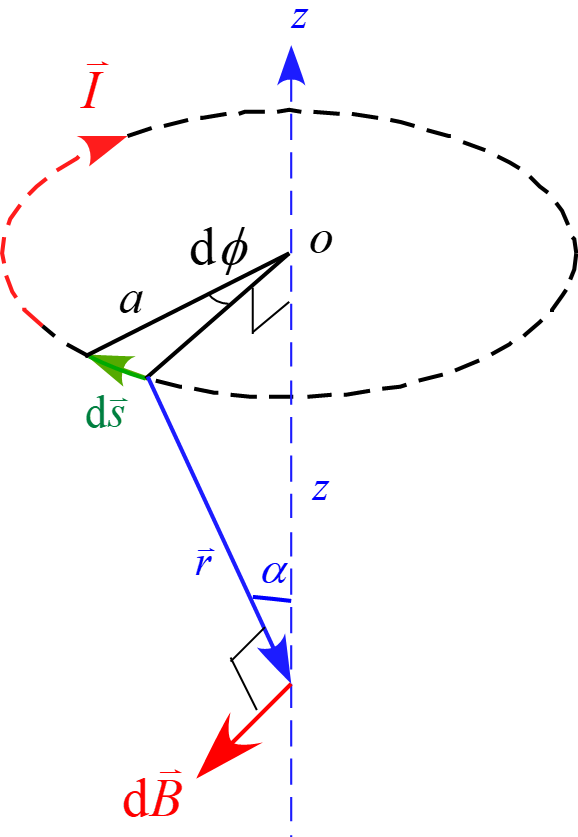
ベクトル部分を抜き出すと下図のようになる。
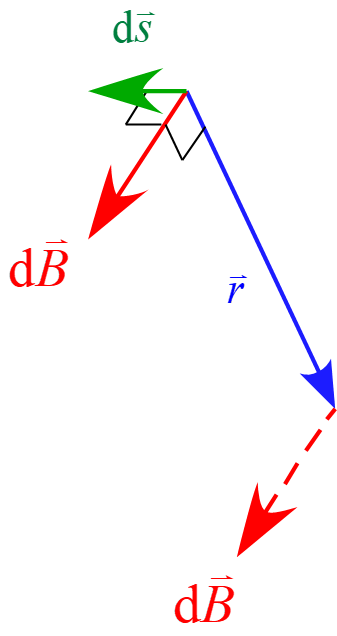
ビオーサバールの法則より、
\begin{eqnarray*}
\diff \vec{B} &=& \frac{\mu_0 }{4\pi} \frac{I \diff \vec{s}}{r^2} \times \frac{\vec{r}}{r} \\
\\
&=& \frac{\mu_0 }{4\pi} \frac{I\ |\diff \vec{s} || \vec{r}| \sin \frac{\pi}{2}}{r^2}\frac{1}{r} \vec{e} \qquad (\vec{e}:\diff \vec{B}\mbox{方向の単位ベクトル})
\\
\\
&=& \frac{\mu_0 }{4\pi} \frac{I\ r\diff s }{r^3} \vec{e}
\end{eqnarray*}
となる。
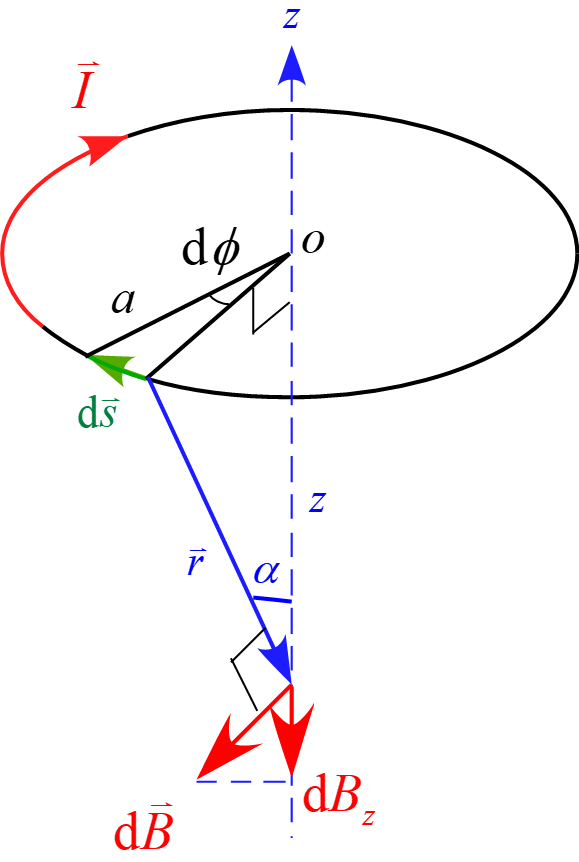
よって、中心軸上に微小部分が作る磁場の大きさ$\diff B_z$は
\begin{eqnarray*}
\diff B_z &=& \diff B \sin \alpha \\
\\
&=& \frac{\mu_0 }{4\pi} \frac{I\ r\ \diff s }{r^3} \sin \alpha \\
\\
&=& \frac{\mu_0 I}{4\pi} \frac{r\ a\diff \phi }{r^3} \frac{a}{r}\\
\\
&=& \frac{\mu_0 I}{4\pi} \frac{a^2}{r^3} \diff \phi \\
\\
&=& \frac{\mu_0 I}{4\pi} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}} \diff \phi
\end{eqnarray*}
となる。
従って求める磁場の大きさ$B_z$は
\begin{eqnarray*}
B_z &=& \int_{0}^{2\pi} \frac{\mu_0 I}{4\pi} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}} \diff \phi \\
\\
&=& \frac{\mu_0 I}{4\pi} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}} \int_{0}^{2\pi} \diff \phi \\
\\
&=& \frac{\mu_0 I}{4\pi} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}} 2\pi \\
\\
&=& \frac{\mu_0 I}{2} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}}
\end{eqnarray*}
となる。
(2)
円形電流の中心地点$z=0$の磁場$B_{z_0}$は
\begin{eqnarray*}
B_{z_0} &=& \frac{\mu_0 I}{2} \frac{a^2}{(a^2 + 0^2)^{\frac{3}{2}}} \\
\\
&=& \frac{\mu_0 Ia^2}{2a^3} \\
\\
&=& \frac{\mu_0 I}{2a} \\
\end{eqnarray*}
となる。
向きは「右向きの法則」より下向きになることが確認できる。
尚、電流$\vec{I}$が「反時計回り」の場合は磁場の大きさは同じで向きが逆になる。