問題
無限に長い直線電流が作る磁場を求めよ。
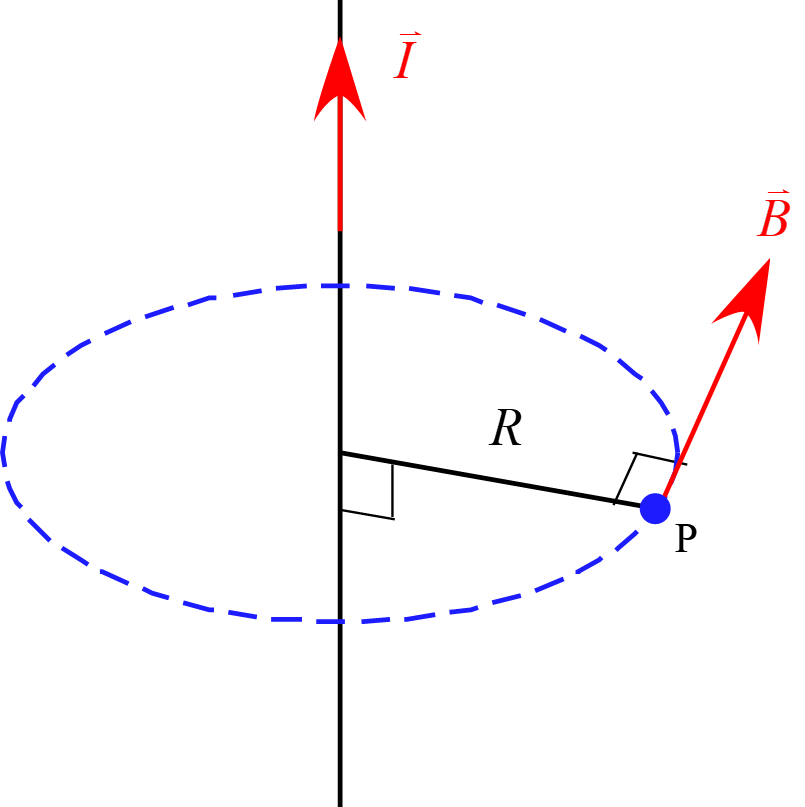
解答
ビオーサバールの法則より電流の微小部分(電流素片)$I \diff \vec{s}$が点Pの位置に作る磁場$d \vec{B}$は
\begin{eqnarray*}
\diff \vec{B} = \frac{\mu_0 }{4\pi} \frac{I \diff \vec{s} \times \vec{r}}{r^3}
\end{eqnarray*}
と表されるので、
直線電流の微小部分が作る電流から距離$R$の位置の磁場の大きさ$\diff B$は$r \sin \theta =R$より
\begin{eqnarray*}
\diff B &=& \frac{\mu_0 I}{4\pi} \frac{\diff z\ r\ \sin \theta}{r^3} \\
\\
&=& \frac{\mu_0 I}{4\pi} \frac{\diff z\ R}{\sqrt{z^2+R^2}^3} \\
\end{eqnarray*}
と表される。
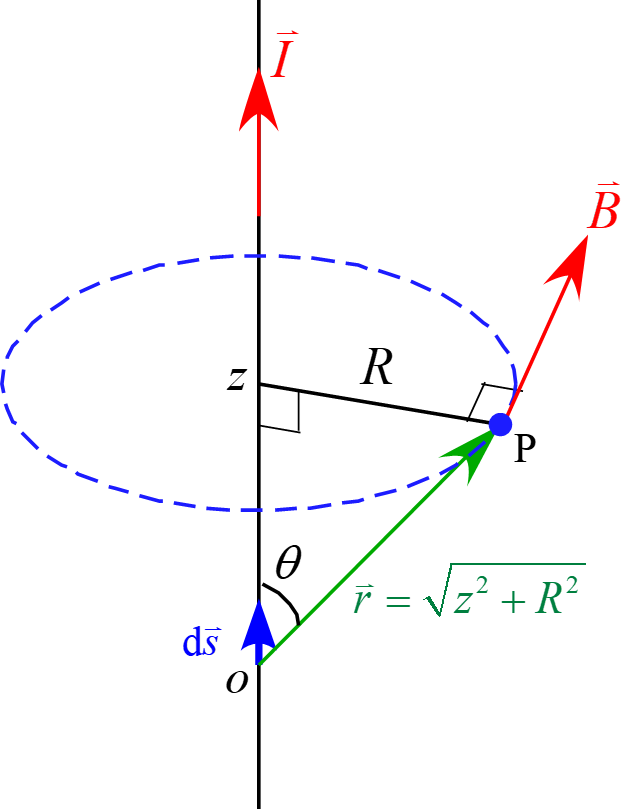
電流は無限に長いので求める磁場$B$は
\begin{eqnarray*}
B &=& \int_{- \infty}^{+ \infty}\frac{\mu_0 IR}{4\pi} \frac{\diff z\ }{(z^2+R^2)^{\frac{3}{2}}} \\
\end{eqnarray*}
を計算することで求められる。
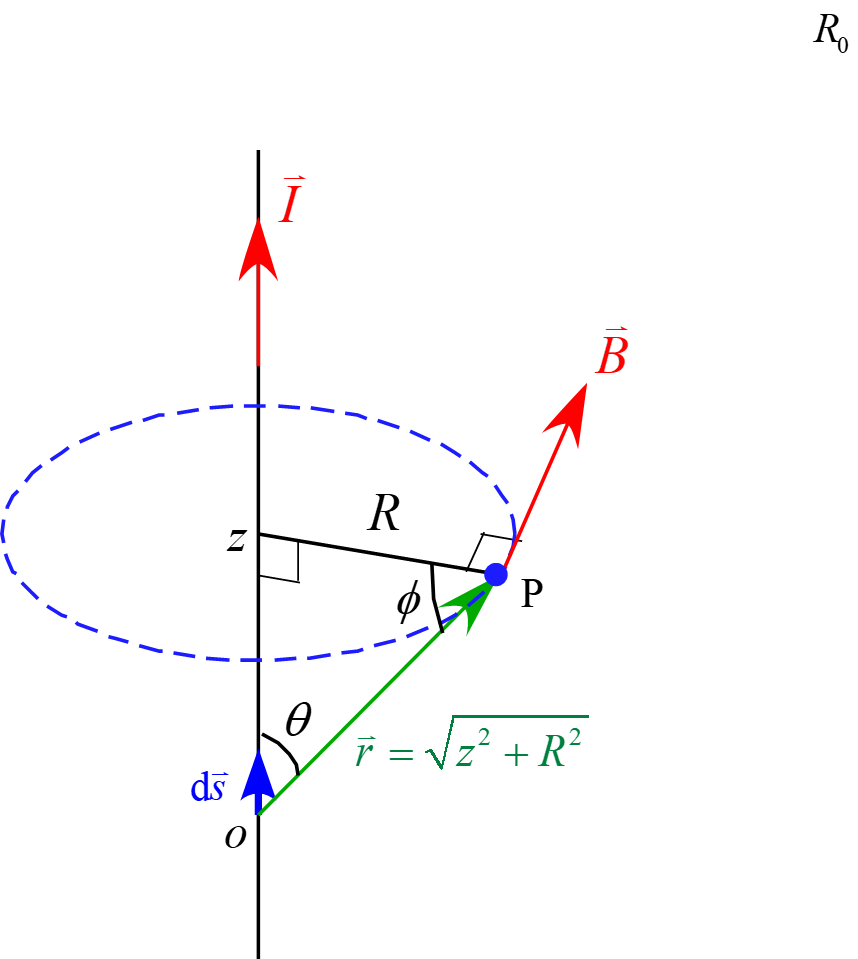
ここで積分変数の$z \to \phi$変換をすると
\begin{eqnarray*}
z &=& R\ \tan \phi \\
\\
\frac{\diff z}{\diff \phi} &=& R\ \frac{1}{\cos^2 \phi}
\\
\cos \phi &=& \frac{R}{r}
\end{eqnarray*}
より
\begin{eqnarray*}
B &=& \frac{\mu_0 IR}{4\pi} \int_{- \infty}^{+ \infty} \frac{\diff z\ }{r^{3}} \\
\\
&=& \frac{\mu_0 IR}{4\pi} \int_{- \frac{\pi}{2}}^{+ \frac{\pi}{2}} \frac{ R \frac{1}{\cos^2 \phi}\diff \theta}{(\frac{R}{\cos \phi})^{3}} \\
\\
&=& \frac{\mu_0 IR}{4\pi} \int_{- \frac{\pi}{2}}^{+ \frac{\pi}{2}} \frac{ R \frac{1}{\cos^2 \phi}\diff \theta}{\frac{R^3}{\cos ^3 \phi}} \\
\\
&=& \frac{\mu_0 I}{4\pi R} \int_{- \frac{\pi}{2}}^{+ \frac{\pi}{2}} \cos \phi\ \diff \phi \\
\\
&=& \frac{\mu_0 I}{4\pi R} \biggl[\sin \phi \biggr]_{- \frac{\pi}{2}}^{+ \frac{\pi}{2}} \\
\\
&=& \frac{\mu_0 I}{4\pi R} \biggl[\sin \frac{\pi}{2} - \sin \biggl( -\frac{\pi}{2} \biggr) \biggr] \\
\\
&=& \frac{\mu_0 I}{4\pi R} \cdot 2 \\
\\
&=& \frac{\mu_0 I}{2\pi R}
\end{eqnarray*}
となる。