導体表面の電場

問題

導体の表面に面密度$\sigma$で電荷が分布しているとき、導体表面の電場の大きさ$E$を求めよ。

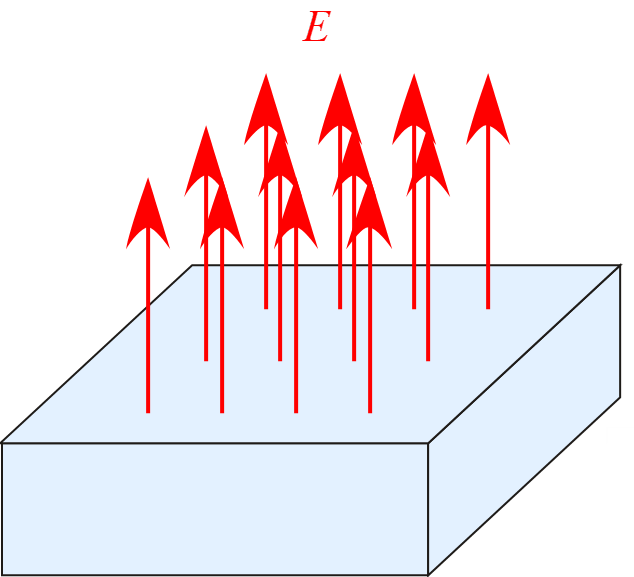
解答

ガウスの法則は

$$\begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\ \\ \int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\ \end{eqnarray*}$$
となるので

導体の表面において図の様な底面積$\Delta S$の円筒形の閉曲面を想定し

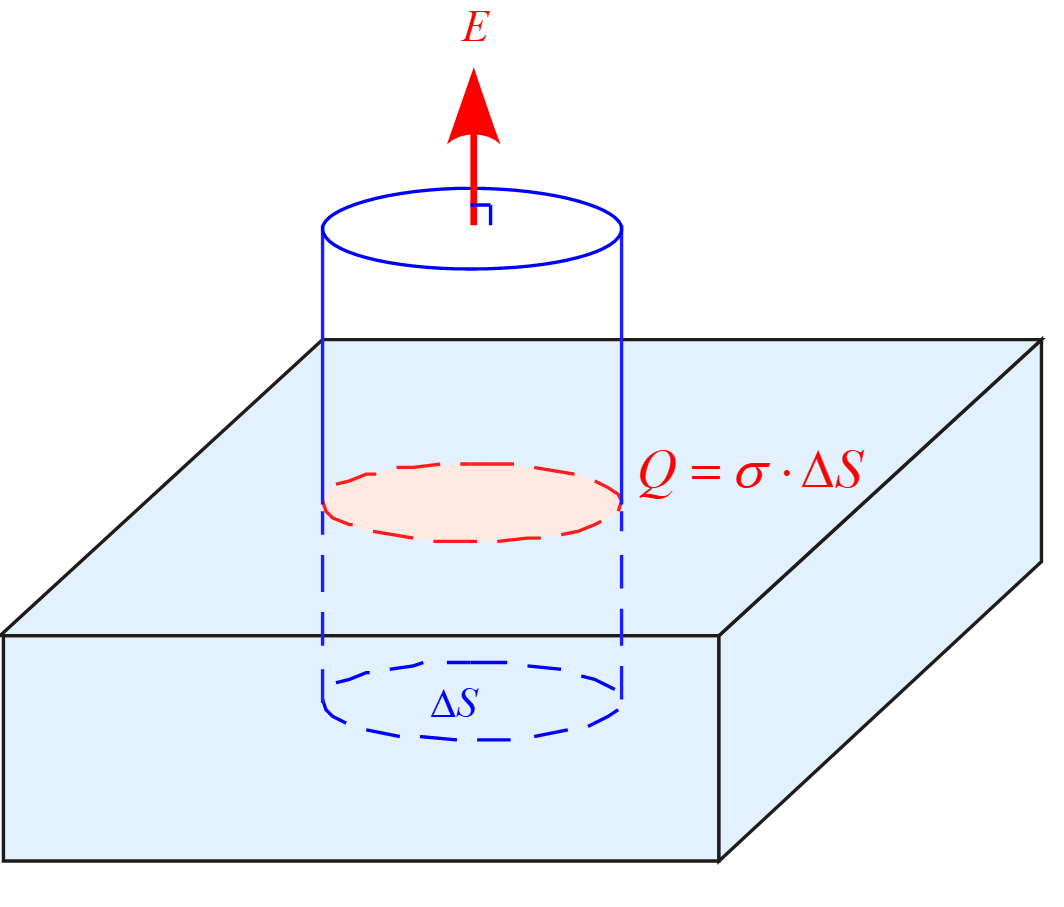
ガウスの法則を適用すると

$$\begin{eqnarray*} \int_{\mbox{円筒上面}} \vec{E} \cdot \vec{n} \diff S + \int_{\mbox{円筒側面}} \vec{E} \cdot \vec{n} \diff S + \int_{\mbox{円筒底面}} \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\ \end{eqnarray*}$$
と表される。

ここで円筒の側面は電場の向きに平行なので$\vec{E}\cdot \vec{n}=0$であり、
また円筒底面は導体内部であるため$E=0$になる。
従って

$$\begin{eqnarray*} \int_{\mbox{円筒上面}} \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\ \\ E \cdot \Delta S &=& \frac{\sigma \cdot \Delta S}{\varepsilon_0} \\ \\ E &=& \frac{\sigma}{\varepsilon_0} \end{eqnarray*}$$
となる。