導体球の電場・電位

問題

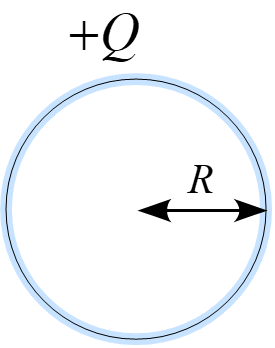
半径$R$の導体球に電荷$+Q$を与えた。以下の問いに答えよ。

(1) 中心からの距離$r$の電場$E(r)$を求め、$E(r)$のグラフを描け。

(2) 中心からの距離$r$の電位$\phi(r)$を求め、$\phi(r)$のグラフを描け。

解答

ガウスの法則は

$$\begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\ \\ \int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\ \end{eqnarray*}$$
となるので

$0 \le r < R$において図の様な半径$r$の球の閉曲面を想定し

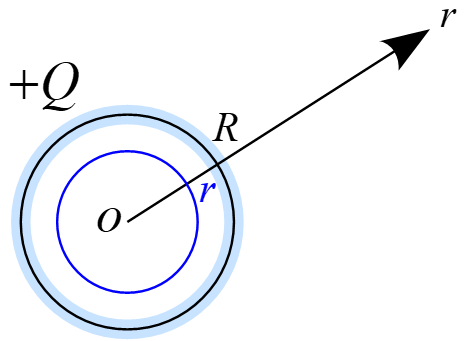
ガウスの法則を適用すると、導体球なので電荷は球の表面のみに分布し、内部には存在しないので

$$\begin{eqnarray*} E(r) \cdot 4 \pi r^2 &=& \frac{0}{\varepsilon_0} \\ \\ E(r) &=& 0 \end{eqnarray*}$$
となる。

$R < r$において図の様な半径$r$の球の閉曲面を想定し

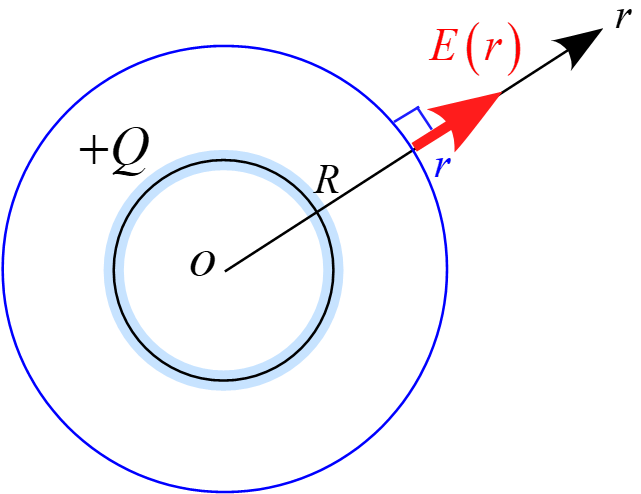
ガウスの法則を適用すると

$$\begin{eqnarray*} E(r) \cdot 4 \pi r^2 &=& \frac{Q}{\varepsilon_0} \\ \\ E(r) &=& \frac{Q}{4 \pi \varepsilon_0} \frac{1}{r^2} \end{eqnarray*}$$
となる。

従って、$E(r)$のグラフは

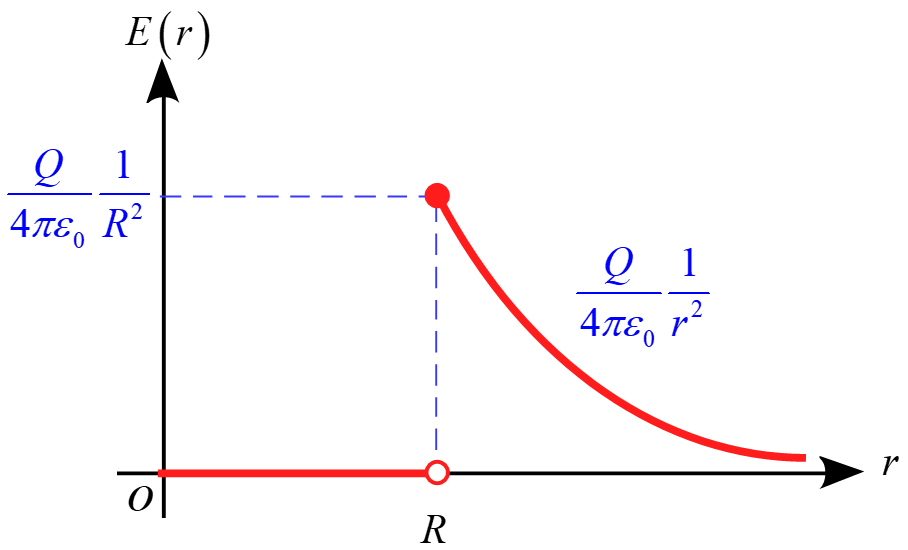
となる。

(2)
$0 \le r < R$において$\phi(r)$は図より$E(r)$のグラフの面積に相当するので

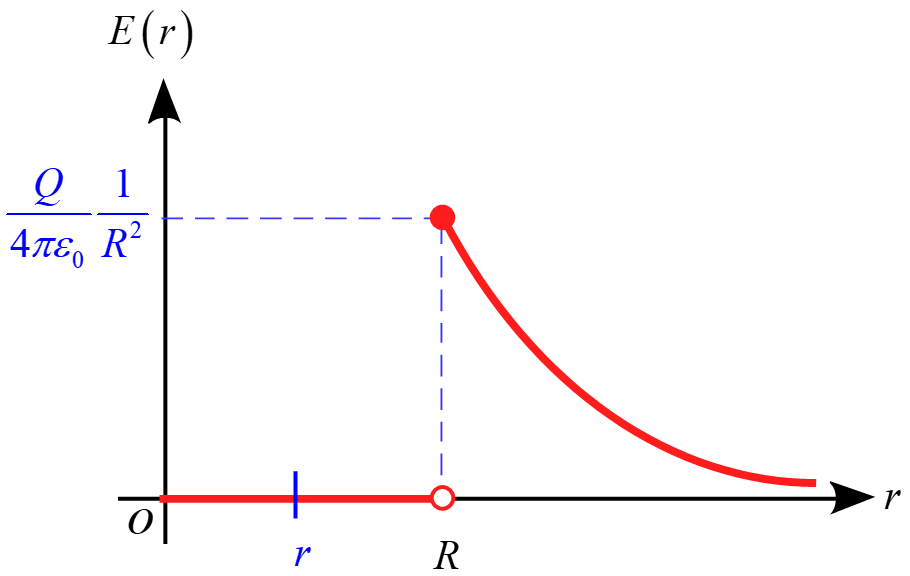
$$\begin{eqnarray*} \phi (r) &=& \int_r^\infty E(r) \diff r\\ \\ &=& 0 + \int_R^\infty E(r) \diff r\\ \\ &=& \int_R^\infty \frac{Q}{4 \pi \varepsilon_0} \frac{1}{r^2} \diff r\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \int_R^\infty \frac{1}{r^2} \diff r\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \biggl[- \frac{1}{r} \biggr]_R^\infty \\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \biggl[- \frac{1}{\infty} - \biggl( -\frac{1}{R} \biggl) \biggr] \\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \frac{1}{R} \end{eqnarray*}$$
となる。

$R < r$においても同様に図より

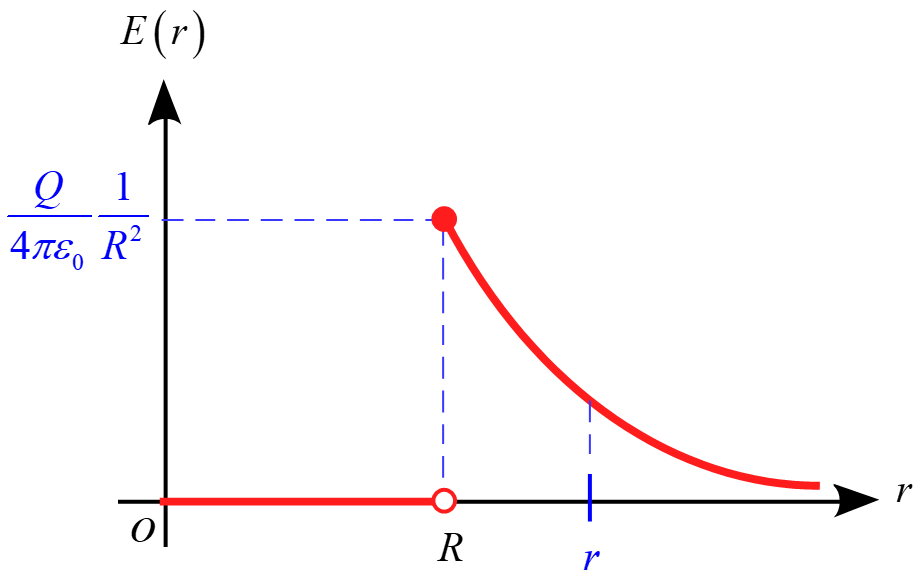
$$\begin{eqnarray*} \phi (r) &=& \int_r^\infty E(r) \diff r\\ \\ &=& \int_r^\infty \frac{Q}{4 \pi \varepsilon_0} \frac{1}{r^2} \diff r\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \int_r^\infty \frac{1}{r^2} \diff r\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \biggl[- \frac{1}{r} \biggr]_r^\infty \\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \biggl[- \frac{1}{\infty} - \biggl( -\frac{1}{r} \biggl) \biggr]\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \frac{1}{r} \end{eqnarray*}$$
となる。

従って、$\phi(r)$のグラフは

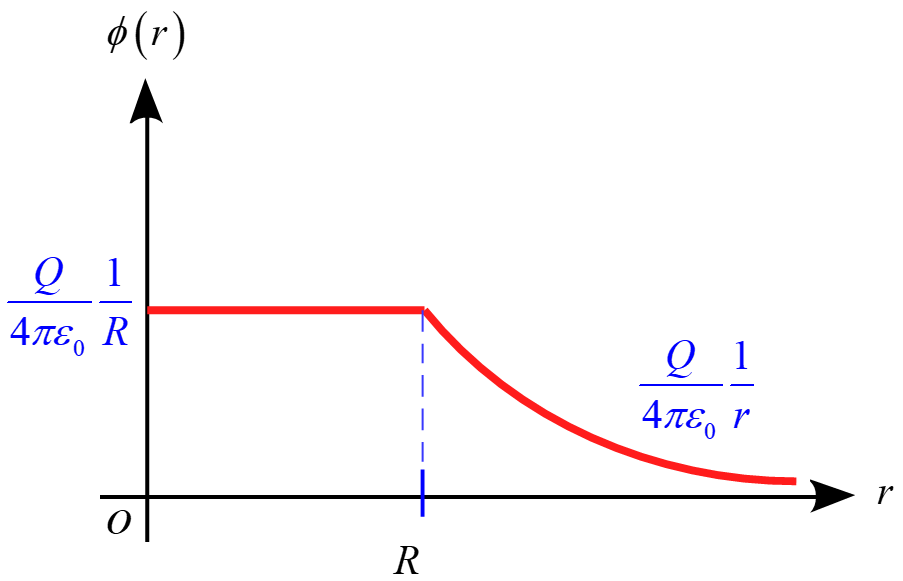
となる。