問題
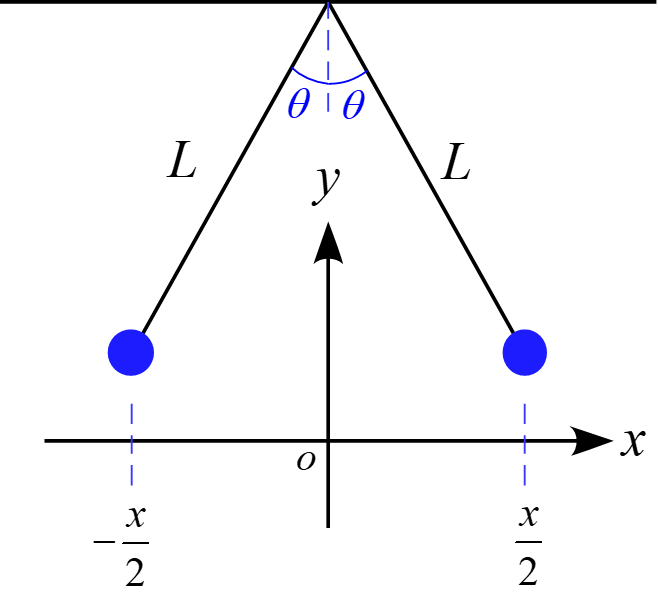
図のように、2本の長さ$L$の糸に質量$m$、電荷$q$を持つ十分に小さな球がそれぞれ吊るされ、静止している。以下の問いに答えよ。ただし、角度$\theta$は十分に小さいものとする。
(1) 運動方程式を記述せよ。
(2) 2つの球の間隔$x$を求めよ。
(1)
物体に作用する力は場の力「重力$mg$」「クーロン力$F_C$」と接触力「張力$T$」となり、右側の小球に着目し座標軸$x,y$に沿って成分を分解すると図の様になる。
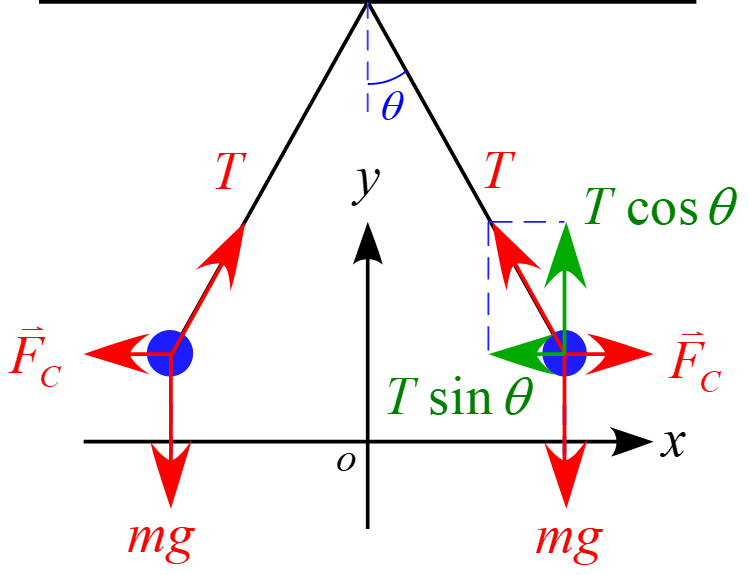
運動方程式は
\begin{eqnarray*}
ma_x &=& F_C-T\sin \theta \\
\\
ma_y &=& T\cos \theta -mg
\end{eqnarray*}
と表される。
初期条件(静止状態)より$a_x=0, a_y=0$なので
\begin{eqnarray*}
0 &=& F_C-T\sin \theta \\
\\
0 &=& T\cos \theta -mg
\end{eqnarray*}
従って
\begin{eqnarray*}
T\sin \theta &=& F_C\\
\\
T\cos \theta &=& mg
\end{eqnarray*}
2式の比を取ると
\begin{eqnarray*}
\frac{T\sin \theta}{T\cos \theta} &=& \frac{F_C}{mg} \\
\\
\tan \theta &=& \frac{F_C}{mg}
\end{eqnarray*}
となる。
ここで、クーロン力$F_C$は
\begin{eqnarray*}
F_C = \frac{1}{4\pi \varepsilon_0}\frac{q^2}{x^2}
\end{eqnarray*}
である。
ここで、糸の長さ$L$と小球の位置$\displaystyle \frac{x}{2}$の位置関係は図の様になる。

従って
\begin{eqnarray*}
\tan \theta &=& \frac{\frac{x}{2}}{\sqrt{L^2 +\biggl(\frac{x}{2} \biggr)^2}} \\
\\
&=& \frac{x}{2} \frac{1}{\sqrt{L^2\biggl[1 + \frac{1}{L^2}\biggl(\frac{x}{2} \biggr)^2}\biggr]} \\
\\
&=& \frac{x}{2} \frac{1}{L\sqrt{1 + \biggl(\frac{x}{2L} \biggr)^2}} \\
\\
&=& \frac{x}{2L} \frac{1}{\sqrt{1 + \biggl(\frac{x}{2L} \biggr)^2}} \\
\end{eqnarray*}
ここで角度$\theta$は十分に小さいので$\displaystyle L \gg x$より$\displaystyle 1 \gg \biggl(\frac{x}{L}\biggr)^2 \simeq 0 $とすると
\begin{eqnarray*}
\tan \theta &\simeq& \frac{x}{2L} \\
\end{eqnarray*}
となる。
従って
\begin{eqnarray*}
\frac{\frac{1}{4\pi \varepsilon_0}\frac{q^2}{x^2}}{mg}= \tan \theta &\simeq& \frac{x}{2L} \\
\\
x^3 &\simeq& \frac{\frac{q^2}{4\pi \varepsilon_0}}{mg}\cdot 2L \\
\\
x^3 &\simeq& \frac{q^2 L}{2\pi \varepsilon_0 mg}\\
\\
x &\simeq& \biggl(\frac{q^2 L}{2\pi \varepsilon_0 mg}\biggr)^{\frac{1}{3}} \\
\end{eqnarray*}
となる。
この結果の変数になり得る部分を抜き出して書き直すと
\begin{eqnarray*}
x &\simeq& \biggl(\frac{1}{2\pi \varepsilon_0 g}\biggr)^{\frac{1}{3}} \frac{q^{\frac{2}{3}} L^{\frac{1}{3}}}{m^{\frac{1}{3}}}
\end{eqnarray*}
と表されます。