問題
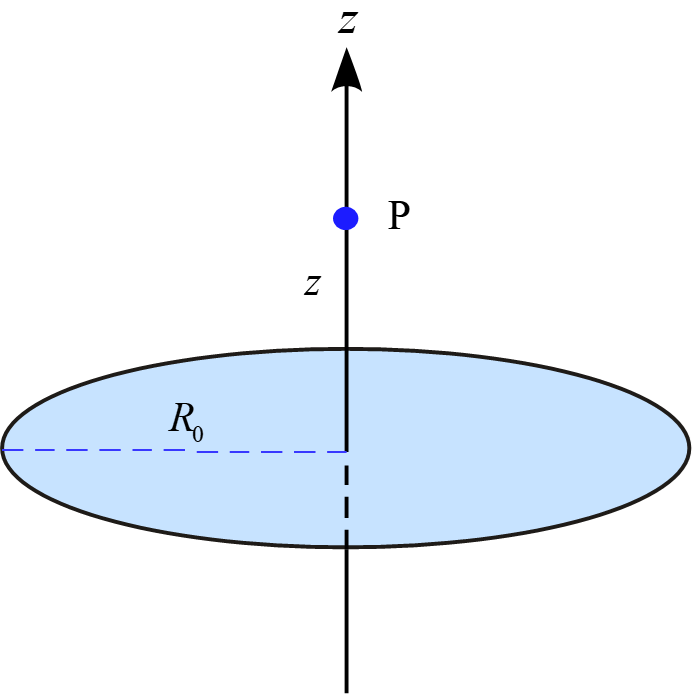
半径$R_0$の円盤に一様な面密度$\sigma$で電荷が帯電している。
以下の問いに答えよ。
(1) 円盤の中心軸上の点P$(0,0,z)$における電位$\phi(z)$を求めよ。
(2) 円盤の中心軸上の点P$(0,0,z)$における電場$E_z$を求めよ。
解答
図のように円盤の中心から半径$R\ (\le R_0)$の場所に幅$\diff R$の微小リングを考える。
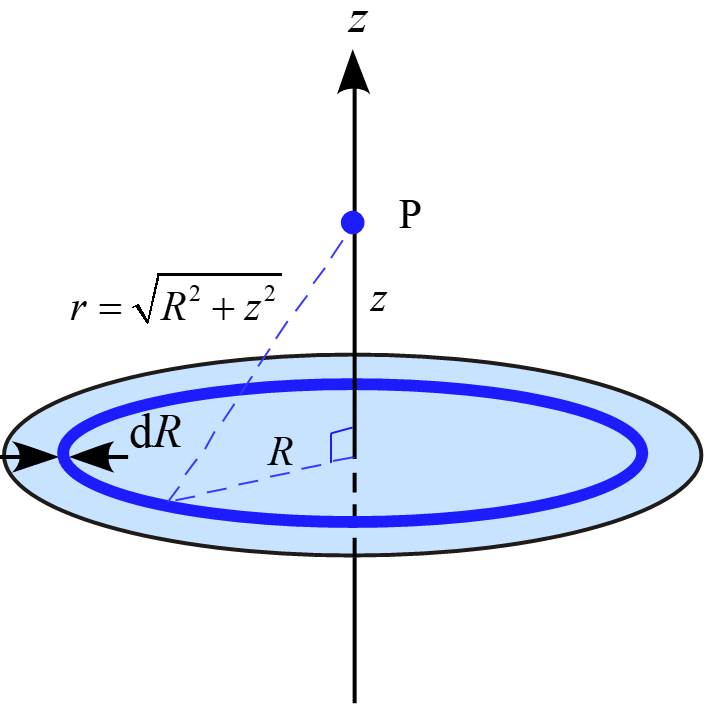
半径$R$の微小リングが持つ電荷$\diff Q$は
\begin{eqnarray*}
\diff Q = 2\pi R \diff R \cdot \sigma
\end{eqnarray*}
となる。
よって、リング状の電荷が作る電位(ポテンシャル)$\diff \phi$は
\begin{eqnarray*}
\diff \phi &=& \frac{1}{4\pi \varepsilon_0} \frac{\diff Q}{r} \\
\\
&=& \frac{1}{4\pi \varepsilon_0} \frac{2\pi R \diff R \cdot \sigma}{\sqrt{R^2+z^2}} \\
\\
&=& \frac{\sigma}{2\varepsilon_0} \frac{R \diff R}{\sqrt{R^2+z^2}}
\end{eqnarray*}
となる。
よって、求める電位$\phi(z)$は
\begin{eqnarray*}
\phi(z) &=& \int_o^{R_0} \frac{\sigma}{2\varepsilon_0} \frac{R \diff R}{\sqrt{z^2+R^2}} \\
\\
&=& \frac{\sigma}{2\varepsilon_0} \int_o^{R_0} \frac{R }{\sqrt{z^2+R^2}}\diff R \\
\\
&=& \frac{\sigma}{2\varepsilon_0} \biggl[ \sqrt{z^2+R^2} \biggr]_0^{R_0} \\
\\
&=& \frac{\sigma}{2\varepsilon_0} (\sqrt{z^2+R_0^2} - \sqrt{z^2+0^2}) \\
\\
&=& \frac{\sigma}{2\varepsilon_0} (\sqrt{z^2+R_0^2} - z)
\end{eqnarray*}
となる。
(2)
(1)の結果より、$z$軸上の電場$E_z$は
\begin{eqnarray*}
E_z =-\frac{\partial \phi(z)}{\partial z} &=& -\frac{\partial}{\partial z} \biggl[ \frac{\sigma}{2\varepsilon_0} (\sqrt{z^2+R_0^2} - z) \biggr] \\
\\
&=& - \frac{\sigma}{2\varepsilon_0} \biggl[ \frac{1}{2} (z^2+R_0^2 )^{-\frac{1}{2}}\cdot 2z -1 \biggr] \\
\\
&=& \frac{\sigma}{2\varepsilon_0} \biggl[1- z (z^2+R_0^2 )^{-\frac{1}{2}} \biggr] \\
\\
&=& \frac{\sigma}{2\varepsilon_0} \biggl( 1 - \frac{z}{\sqrt{z^2 + R_0^2}} \biggr)
\end{eqnarray*}
となる。