問題
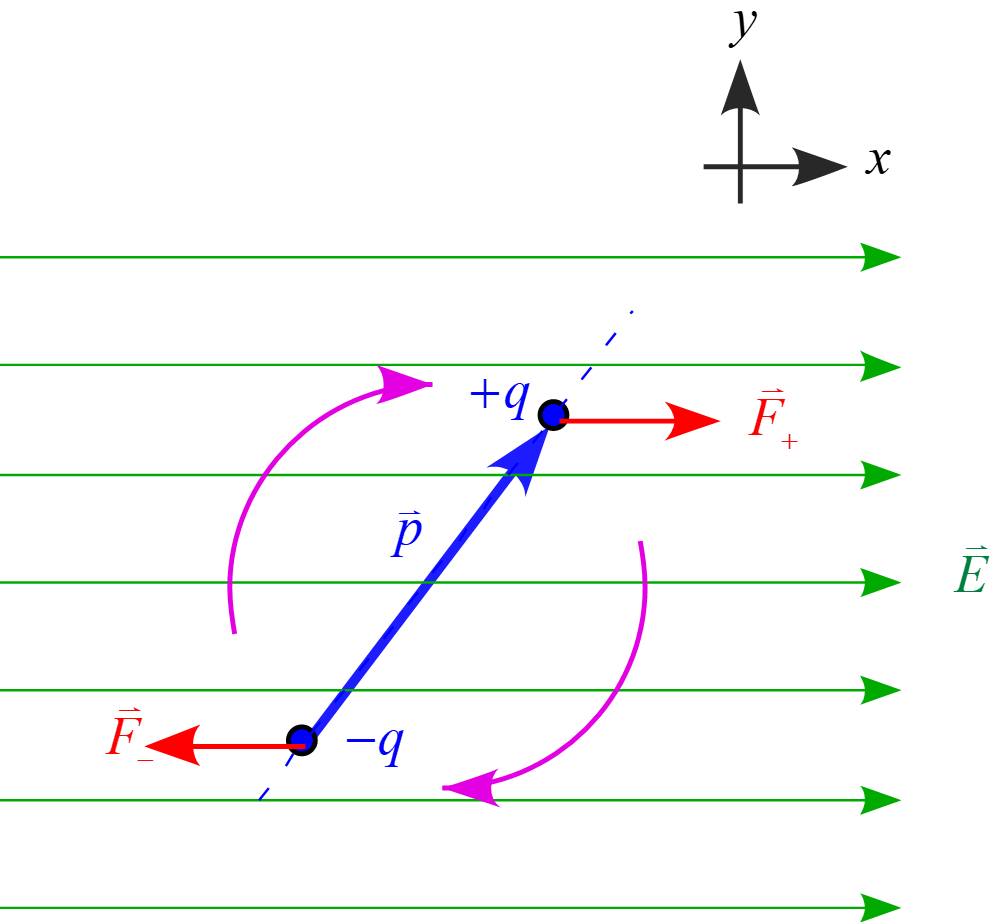
一様な電場 $\vec{E}$ が存在する空間に、電荷がそれぞれ $\pm q$ である電気双極子を置いたとする。以下の問いに答えよ。ただし、2つの電荷の間の距離は $d$ とする。
(1) 電気双極子が受ける力のモーメント$\vec{M}$を求めよ。
(2) 電気双極子が受ける力のモーメント$\vec{M}$を外積を用いて表せ。
解答
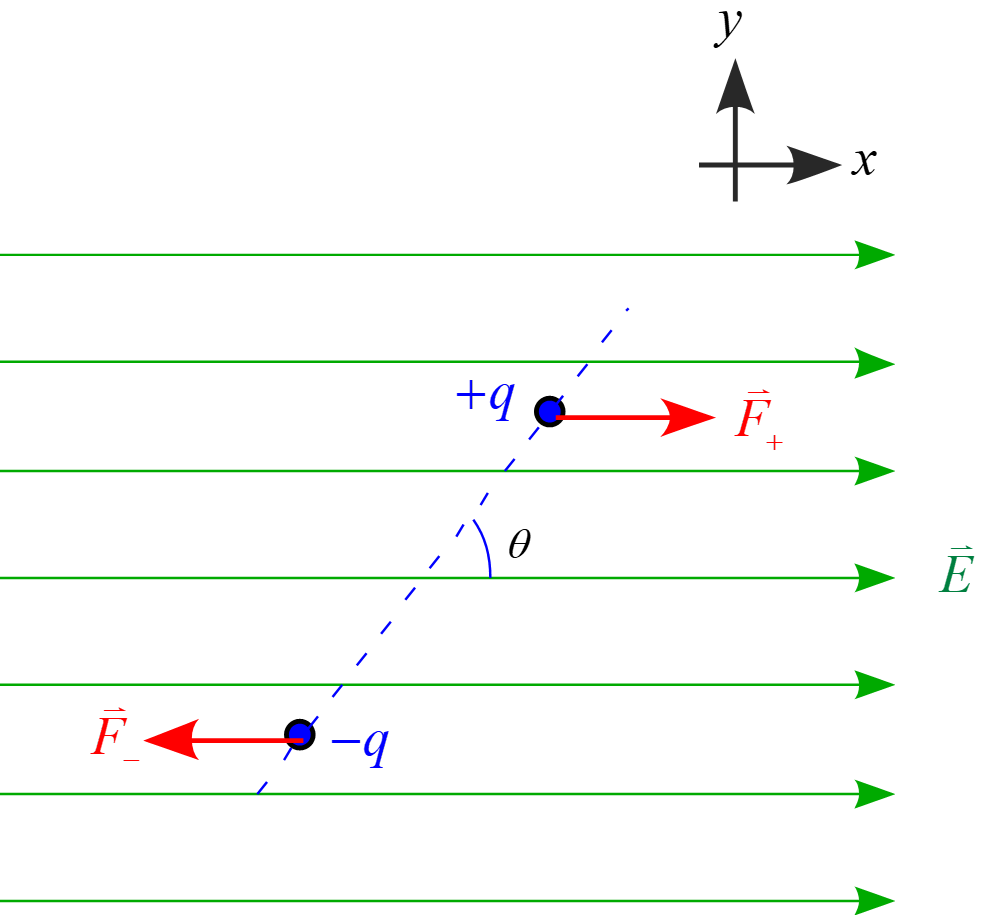
図の様に電場の向きと$x$軸が一致するように座標軸$x,y$を設定する。
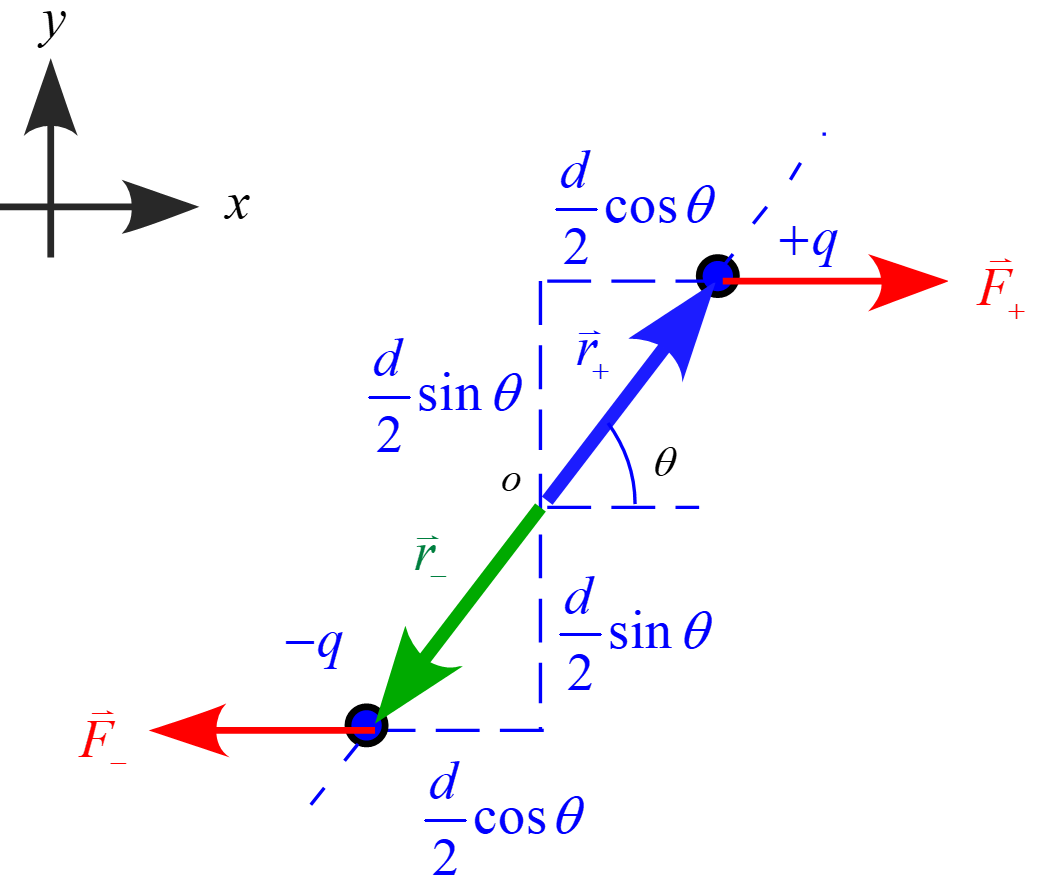
(1)
電気双極子の2つの電荷の中央を支点にし、それぞれの電荷に作用する力のモーメントは
$+q$の電荷について、位置ベクトル$\vec{r_+}$と作用する力$\vec{F_+}$は
\begin{eqnarray*}
\vec{r_+} =
\left(
\begin{array}{c}
\frac{d}{2} \cos \theta \\
\frac{d}{2} \sin \theta \\
0
\end{array}
\right) ,\qquad
\vec{F_+} =
\left(
\begin{array}{c}
qE \\
0 \\
0
\end{array}
\right) \\
\end{eqnarray*}
と表されるので
力のモーメント$\vec{M_+}$は
\begin{eqnarray*}
\vec{M_+} =\vec{r_+} \times \vec{F_+} &=&
\left(
\begin{array}{c}
\frac{d}{2} \cos \theta \\
\frac{d}{2} \sin \theta \\
0
\end{array}
\right) \times
\left(
\begin{array}{c}
qE \\
0 \\
0
\end{array}
\right) \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
\frac{d}{2} \cos \theta \cdot 0 - \frac{d}{2} \sin \theta \cdot qE
\end{array}
\right) \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
- \frac{dqE}{2} \sin \theta
\end{array}
\right) \\
\end{eqnarray*}
となり、力のモーメントの大きさ$|\vec{M_+}|$は
\begin{eqnarray*}
|\vec{M_+}| = \sqrt{0^2 +0^2 + \biggl(- \frac{dqE}{2} \sin \theta \biggr)^2} = \frac{dqE}{2} \sin \theta\\
\end{eqnarray*}
となる。
$-q$の電荷についても同様に、位置ベクトル$\vec{r_-}$と作用する力$\vec{F_-}$は
\begin{eqnarray*}
\vec{r_-} =
\left(
\begin{array}{c}
-\frac{d}{2} \cos \theta \\
-\frac{d}{2} \sin \theta \\
0
\end{array}
\right) ,\qquad
\vec{F_-} =
\left(
\begin{array}{c}
-qE \\
0 \\
0
\end{array}
\right) \\
\end{eqnarray*}
と表され、
力のモーメント$\vec{M_-}$は
\begin{eqnarray*}
\vec{M_-} =\vec{r_-} \times \vec{F_-} &=&
\left(
\begin{array}{c}
-\frac{d}{2} \cos \theta \\
-\frac{d}{2} \sin \theta \\
0
\end{array}
\right) \times
\left(
\begin{array}{c}
-qE \\
0 \\
0
\end{array}
\right) \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
-\frac{d}{2} \cos \theta \cdot 0 - \biggr(-\frac{d}{2} \sin \theta\biggr) \cdot -qE
\end{array}
\right) \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
- \frac{dqE}{2} \sin \theta
\end{array}
\right) \\
\end{eqnarray*}
となるので、力のモーメントの大きさ$|\vec{M_-}|$は
\begin{eqnarray*}
|\vec{M_-}| = \sqrt{0^2 +0^2 + \biggl(- \frac{dqE}{2} \sin \theta \biggr)^2} = \frac{dqE}{2} \sin \theta \\
\end{eqnarray*}
となる。
従って、この電気双極子が受ける力のモーメント$\vec{M}$は
\begin{eqnarray*}
\vec{M} &=& \vec{M_+} + \vec{M_-} \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
- \frac{dqE}{2} \sin \theta
\end{array}
\right)
+
\left(
\begin{array}{c}
0 \\
0 \\
- \frac{dqE}{2} \sin \theta
\end{array}
\right) \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
- qdE \sin \theta
\end{array}
\right) \\
\end{eqnarray*}
と表される。
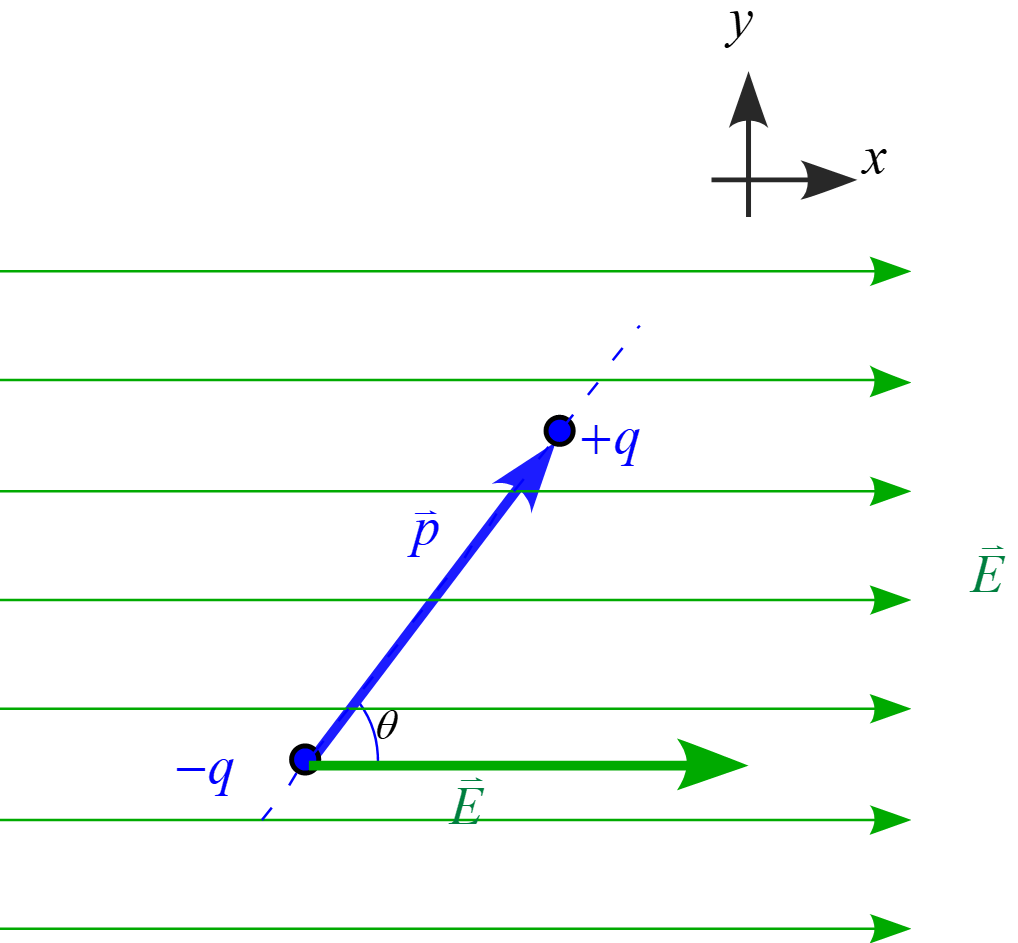
(2)
これは電気双極子モーメント$\vec{p}=q\vec{d}$と表すと
\begin{eqnarray*}
\vec{p}= q\left(
\begin{array}{c}
d \cos \theta \\
d \sin \theta \\
0
\end{array}
\right) \\
\end{eqnarray*}
であり、
\begin{eqnarray*}
\vec{M}=\vec{p} \times \vec{E}
&=& q\left(
\begin{array}{c}
d \cos \theta \\
d \sin \theta \\
0
\end{array}
\right) \times
\left(
\begin{array}{c}
E \\
0 \\
0
\end{array}
\right) \\
\\
&=& q \left(
\begin{array}{c}
0 \\
0 \\
d \cos \theta \cdot 0 - E\cdot d \sin \theta
\end{array}
\right) \\
\\
&=& \left(
\begin{array}{c}
0 \\
0 \\
- qdE\sin \theta
\end{array}
\right) \\
\end{eqnarray*}
となる結果と一致する。
従って、電気双極子が受ける力のモーメント$\vec{M}$を外積を用いて表すと
\begin{eqnarray*}
\vec{M}=\vec{p} \times \vec{E}
\end{eqnarray*}
となる。
尚、$z$成分のマイナスはこの回転が「時計回り」であることを示している。