問題
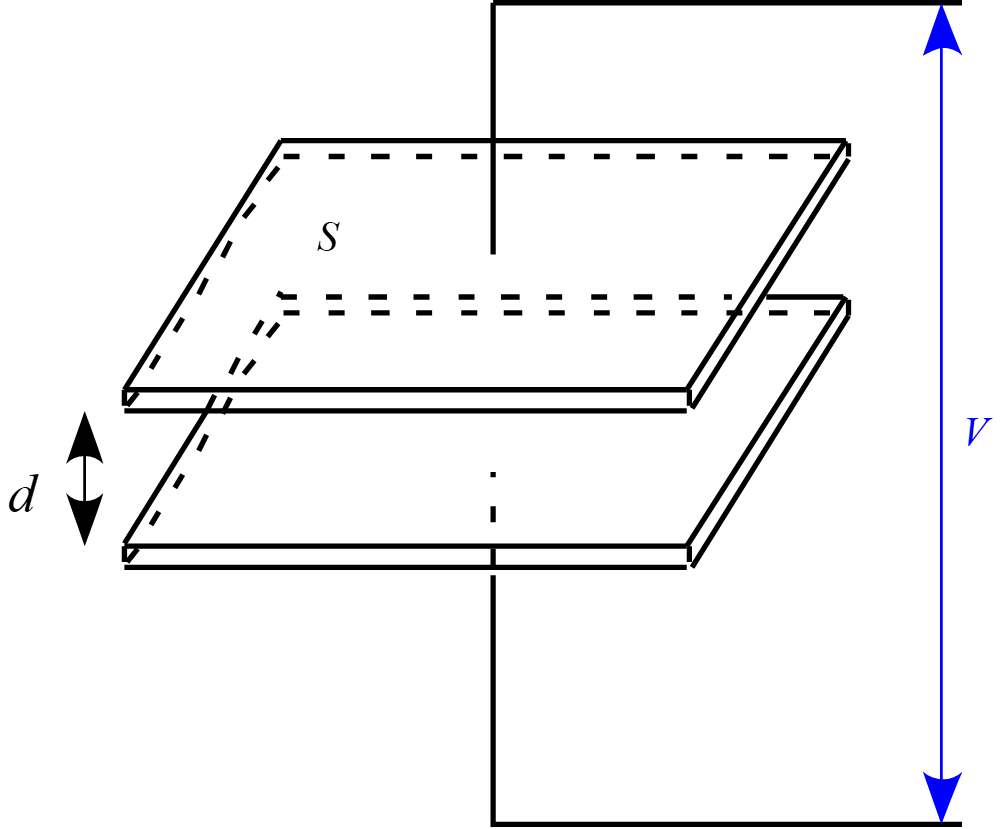
図のような面積 $S$、極板間距離 $d$ の平行板コンデンサーを考える。
ただし、電極間の誘電率は$\varepsilon_0$とする。
(1) 電荷が一様な状態で分布し面密度$\sigma$であるとき電極間の電場$E$を求めよ。
(2) このコンデンサーの静電容量を求めよ。
解答
(1)
コンデンサーの両端に$+Q,\ -Q$の電荷を与えるとすると、電荷$Q$は
\begin{eqnarray*}
Q = \sigma S
\end{eqnarray*}
で表される。
ガウスの法則は
\begin{eqnarray*}
\int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\
\\
\int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\
\end{eqnarray*}
となるので
コンデンサーにおいて図の様な閉曲面を想定し
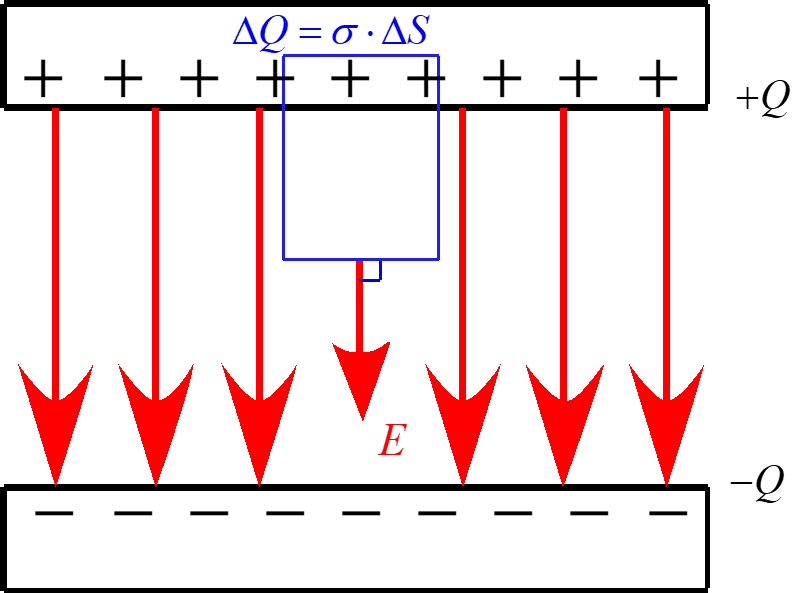
ガウスの法則を適用すると
\begin{eqnarray*}
E \cdot \Delta S &=& \frac{\Delta Q}{\varepsilon_0} \\
\\
E \cdot \Delta S &=& \frac{\sigma \Delta S}{\varepsilon_0} \\
\\
&=& \frac{\sigma}{\varepsilon_0} \\
\end{eqnarray*}
となる。(参照:導体表面の電場)
(2)
電位$V$と電場$E$の関係は$1 \mbox{C}$当たりの仕事を考えると
\begin{eqnarray*}
V=E\cdot d
\end{eqnarray*}
と表されるので
\begin{eqnarray*}
E = \frac{V}{d}
\end{eqnarray*}
となる。
(1)の結果と合わせると
\begin{eqnarray*}
E = \frac{\sigma}{\varepsilon_0} = \frac{V}{d}
\end{eqnarray*}
となる。
コンデンサーに蓄えられる電荷$Q$は$Q=\sigma S$で表されるので、
\begin{eqnarray*}
\frac{Q}{\varepsilon_0 S} &=& \frac{V}{d} \\
\\
Q &=& \frac{\varepsilon_0 S}{d} V
\end{eqnarray*}
と表される。
$Q$は$V$に比例し、その比例定数が静電容量$C$であるから
\begin{eqnarray*}
C = \frac{\varepsilon_0 S}{d}
\end{eqnarray*}
となる。