地球の静電容量

問題

地球を孤立した導体球と仮定し、以下の問いに答えよ。但し、地球の半径は $R_E = 6.38 \times 10^6 \ \mathrm{m}$、真空の誘電率は $\varepsilon_0 = 8.85 \times 10^{-12} \ \mathrm{F/m}$ とする。

(1) 地球の中心からの距離$r\ (> R_E)$における電場$E(r)$を求めよ。

(2) 地球の中心からの距離$r\ (> R_E)$における電位$\phi(r)$を求めよ。

(3) 地球の静電容量$C_E$を求めよ。

解答

(1)
ガウスの法則は

$$\begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\ \\ \int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\ \end{eqnarray*}$$
となるので

$R_E \le r$において図の様な半径$r$の球の閉曲面を想定し

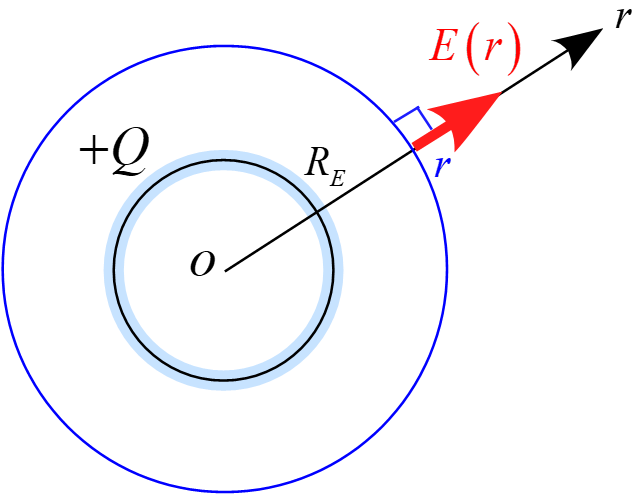
ガウスの法則を適用すると

$$\begin{eqnarray*} E(r) \cdot 4 \pi r^2 &=& \frac{Q}{\varepsilon_0} \\ \\ E(r) &=& \frac{Q}{4 \pi \varepsilon_0} \frac{1}{r^2} \end{eqnarray*}$$
となる。

(2)
$R_E \le r$において導体球の電位$\phi(r)$は

$$\begin{eqnarray*} \phi (r) &=& - \int_\infty^{R_{E}} E(r) \diff r\\ \\ &=& \int_{R_{E}}^\infty E(r) \diff r\\ \\ &=& \int_{R_E}^\infty \frac{Q}{4 \pi \varepsilon_0} \frac{1}{r^2} \diff r\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \int_{R_E}^\infty \frac{1}{r^2} \diff r\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \biggl[- \frac{1}{r} \biggr]_{R_E}^\infty \\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \biggl[- \frac{1}{\infty} - \biggl( -\frac{1}{{R_E}} \biggl) \biggr]\\ \\ &=& \frac{Q}{4 \pi \varepsilon_0} \frac{1}{{R_E}} \end{eqnarray*}$$
となる。

(3)
地球の静電容量$C_E$は

$$\begin{eqnarray*} C_E &=& \frac{Q}{\phi} \\ \\ &=& \frac{Q}{\frac{Q}{4 \pi \varepsilon_0} \frac{1}{{R_E}}} \\ \\ &=& 4\pi \varepsilon_0 R_E \\ \\ &=& 4 \times \pi \times 8.85 \times 10^{-12}\ \mathrm{F/m} \times 6.38 \times 10^{6}\ \mathrm{m} \\ \\ &\simeq& 7.095 \times 10^{-4}\ \mathrm{F}\\ \\ &\simeq& 710 \ \mu \mathrm{F}\\ \end{eqnarray*}$$

となる。(有効数字は与えられた数値の有効数字3桁とした)