問題
$z$ 軸を中心軸とし、内側の半径が $a$、外側の半径が $b$ である金属製の筒を用いて、同軸円筒型コンデンサーを考える。ただし、$a < b$ とする。
(1) 2つの筒に電位差 $V$ を与えたとき、単位長さ当たりの電荷 $\rho$ を求めよ。
(2) このコンデンサーの単位長さ当たりの静電容量 $C_L$ を求めよ。
解答
(1)
ガウスの法則は
\begin{eqnarray*}
\int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\
\\
\int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\
\end{eqnarray*}
なので
$a < r < b $において図の様な半径$r$、高さ$Z$の円柱の閉曲面を想定し
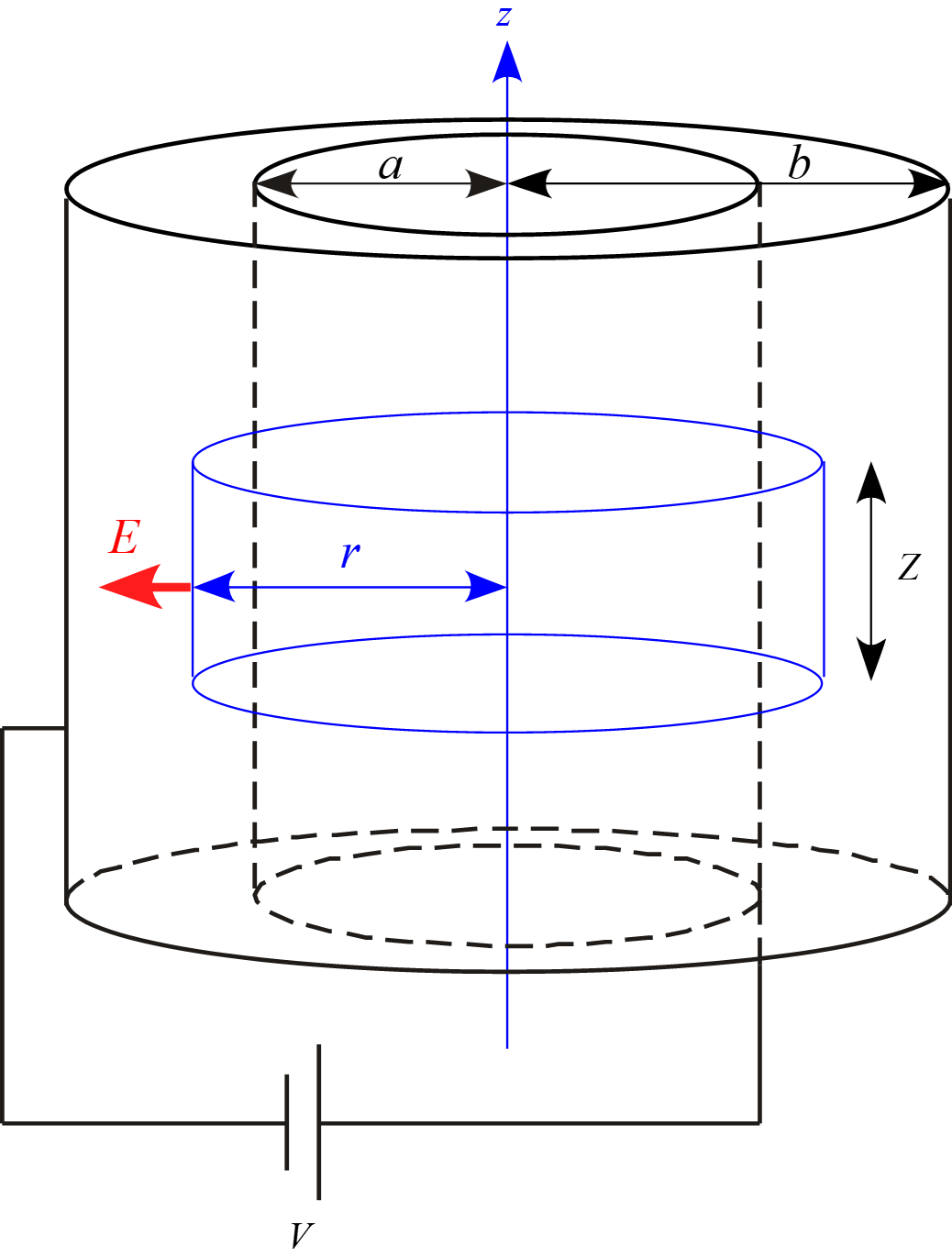
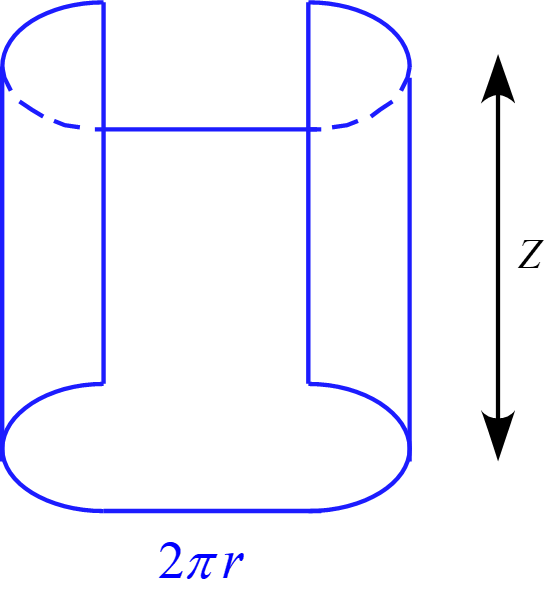
ガウスの法則を適用すると
\begin{eqnarray*}
E(r) \cdot 2 \pi r Z &=& \frac{\rho Z}{\varepsilon_0} \\
\\
E(r) &=& \frac{\rho}{2 \pi \varepsilon_0} \frac{1}{r}
\end{eqnarray*}
となる。
よって電位$V$は
\begin{eqnarray*}
V &=& - \int_b^a E \diff r \\
\\
&=& - \int_b^a \frac{\rho}{2 \pi \varepsilon_0} \frac{1}{r} \diff r \\
\\
&=& - \frac{\rho}{2 \pi \varepsilon_0} \int_b^a \frac{1}{r} \diff r \\
\\
&=& - \frac{\rho}{2 \pi \varepsilon_0} \biggl[ \log r \biggr]_b^a \\
\\
&=& - \frac{\rho}{2 \pi \varepsilon_0} \bigl( \log a - \log b \bigr) \\
\\
&=& \frac{\rho}{2 \pi \varepsilon_0} \bigl( \log b - \log a \bigr) \\ \\
\\
&=& \frac{\rho}{2 \pi \varepsilon_0} \log \frac{b}{a}
\end{eqnarray*}
と計算される。
従って、単位長さ当たりの電荷$\rho$は
\begin{eqnarray*}
\rho = \frac{2\pi \varepsilon_0}{\log \frac{b}{a}} V
\end{eqnarray*}
となる。
(2)
単位長さ当たりの静電容量$C_L$は$Q=CV$より
\begin{eqnarray*}
\rho &=& C_L V \\
\\
C_L &=& \frac{\rho}{V} \\
\\
&=& \frac{\frac{2\pi \varepsilon_0}{\log \frac{b}{a}} V}{V} \\
\\
&=& \frac{2\pi \varepsilon_0}{\log \frac{b}{a}}
\end{eqnarray*}
となる。
注)
単位長さ当たりになっても電位差$V$は変わらない