問題
電流が周期的に変動し$I(t) = I_0 \sin (2\pi ft)$で与えられるとする。
以下の問いに答えよ。
(1) 抵抗$R$に流したときの平均仕事率$\bar{P}$を求めよ。
(2) この回路の平均電流を求めよ。
解答
(1)
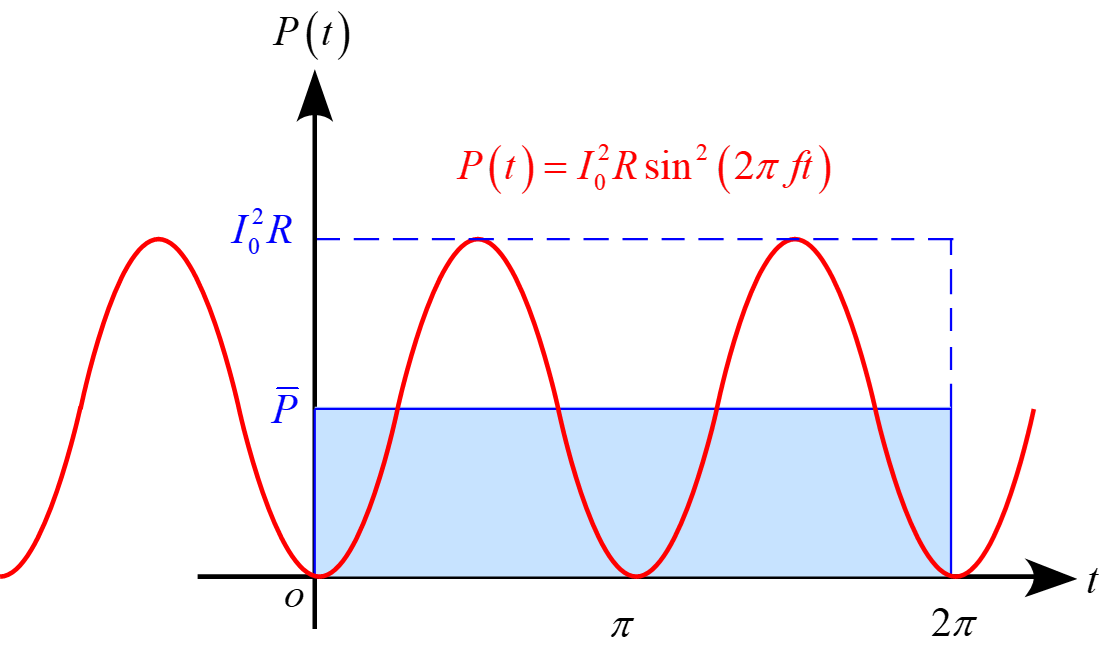
仕事率$P$は
\begin{eqnarray*}
P =I^2 R &=& \biggl[I_0 \sin(2\pi f t)\biggr]^2 R \\
\\
&=& I_0^2 R \sin^2(2\pi ft)
\end{eqnarray*}
と表されるので平均仕事率$\bar{P}$は
\begin{eqnarray*}
\bar{P} &=& \frac{1}{T} \int_0^T I_0^2 R \sin^2(2\pi ft) \diff t \\
\\
&=& \frac{I_0^2 R}{T} \int_0^T \sin^2(2\pi ft) \diff t \\
\\
&=& \frac{I_0^2 R}{T} \int_0^T \frac{1-\cos(2 \cdot 2\pi f t)}{2} \diff t \\
\\
&=& \frac{I_0^2 R}{2T} \int_0^T [1 -\cos(4\pi f t))] \diff t \\
\\
&=& \frac{I_0^2 R}{2T} \biggl[t - \frac{1}{4\pi f} \sin(4\pi f t) \biggr]_0^T \\
\\
&=& \frac{I_0^2 R}{2T} \biggl[T - \frac{1}{4\pi f} \sin(4\pi f T) - \{0 - \frac{1}{4\pi f} \sin(4\pi f \cdot 0)\} \biggr] \\
\\
&=& \frac{I_0^2 R}{2T} T \\
\\
&=& \frac{1}{2}I_0^2 R
\end{eqnarray*}
となる。
(2)
平均電流$\bar{I}$は
\begin{eqnarray*}
I (t) &=& I_0 \sin(2\pi f t) \\
\\
I^2(t) &=& I_0^2 \sin^2(2\pi ft) \\
\end{eqnarray*}
より
\begin{eqnarray*}
\bar{I}^2(t) &=& \frac{1}{T} \int_0^T I_0^2 \sin^2(2\pi ft) \diff t \\
\\
&=& \frac{I_0^2}{T} \int_0^T \sin^2(2\pi ft) \diff t \\
\\
&=& \frac{I_0^2}{T} \int_0^T \frac{1-\cos(2\cdot 2\pi ft)}{2} \diff t \\
\\
&=& \frac{I_0^2}{2T} \int_0^T \bigl[ 1 - \cos(4\pi ft) \bigr] \diff t \\
\\
&=& \frac{I_0^2}{2T} \biggl[ t - \frac{1}{4\pi f} \sin(4\pi ft) \biggr]_0^T \\
\\
&=& \frac{I_0^2}{2T} \biggl[ T - \frac{1}{4\pi f} \sin(4\pi fT) - \{ 0 - \frac{1}{4\pi f} \sin(4\pi f\cdot 0)\} \biggr] \\
\\
&=& \frac{I_0^2}{2T} T \\
\\
&=& \frac{I_0^2}{2}
\end{eqnarray*}
となる。
従って、電流の平均自乗偏差$I_{\mbox{rms}}$は
\begin{eqnarray*}
I_{\mbox{rms}} = \sqrt{\bar{I^2}}= \sqrt{\frac{I_o^2}{2}}= \frac{1}{\sqrt{2}}I_0
\end{eqnarray*}
となる。