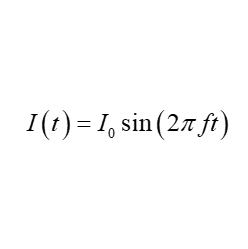kawa

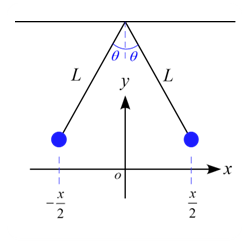
問題 図のように、2本の長さ$L$の糸に質量$m$、電荷$q$を持つ十分に小さな球がそれぞれ吊るされ、静止している。以下の問いに答えよ。ただし、角度$\theta$は十分に小さいものとする。 (1) 運動方程式を記述せよ。 (2) 2つの球の間隔$x$を求めよ。 (1) 物体に作用する力は場の力「重力$mg$」「クーロン力$F_C$」と接触力「張力$T$」となり、右側の小球に着目し座標軸$x,y$に沿って成分を分解すると図の様になる。 運動方程式は \begin{eqnarray*} ma_x &=& F ...

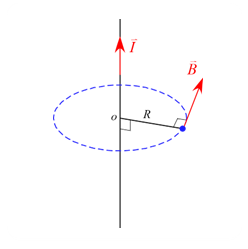
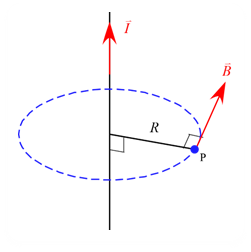
問題 無限に長い直線電流$\vec{I}$が作る磁場を求めよ。 解答 アンペールの法則を適用する閉曲面$S$を電流$\vec{I}$が中心を通る半径$R$の円に設定すると アンペールの法則 \begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\ \\ \mbox{閉曲面$S$の縁$C$に沿っての磁場の線積分} &=& \mu_0 \times \mbox{閉曲面 ...

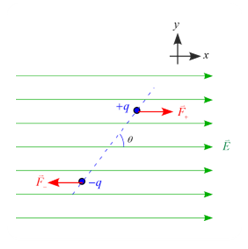
問題 一様な電場 $\vec{E}$ が存在する空間に、電荷がそれぞれ $\pm q$ である電気双極子を置いたとする。以下の問いに答えよ。ただし、2つの電荷の間の距離は $d$ とする。 (1) 電気双極子が受ける力のモーメント$\vec{M}$を求めよ。 (2) 電気双極子が受ける力のモーメント$\vec{M}$を外積を用いて表せ。 解答 図の様に電場の向きと$x$軸が一致するように座標軸$x,y$を設定する。 (1) 電気双極子の2つの電荷の中央を支点にし、それぞれの電荷に作用する力のモーメントは ...

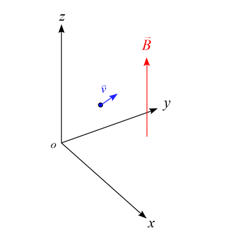
問題 $z$軸方向に一様な磁場$\vec{B}$がある。この磁場内で運動する荷電粒子について論ぜよ。但し、荷電粒子の質量$m$、電荷を$q$とする。 解答 一様な磁場内$\vec{B}$で運動する荷電粒子に作用する力はローレンツ力が作用するので運動方程式は \begin{eqnarray*} m \frac{\diff \vec{v}}{\diff t} = q(\vec{v} \times \vec{B}) \end{eqnarray*} と表される。 成分で表すと \begin{eqnarray*} ...

問題 電流が周期的に変動し$I(t) = I_0 \sin (2\pi ft)$で与えられるとする。 以下の問いに答えよ。 (1) 抵抗$R$に流したときの平均仕事率$\bar{P}$を求めよ。 (2) この回路の平均電流を求めよ。 解答 (1) 仕事率$P$は \begin{eqnarray*} P =I^2 R &=& \biggl[I_0 \sin(2\pi f t)\biggr]^2 R \\ \\ &=& I_0^2 R \sin^2(2\pi ft) \end{eqnarray*} と表される ...

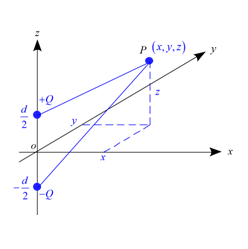
問題 $z$軸上に点電荷$\pm Q$が距離$d$離れて置かれている。この距離$d$の中心を原点として以下の問いに答えよ。但し$d \ll r$とする。 (1) 点P$(x,y,z)$においてこの2つの電荷が作る電位$\phi$を求めよ。 (2) 点P$(x,y,z)$においこの2つの電荷が作る電場$E$を求めよ。 解答 (1) それぞれの電荷が作る電位は \begin{eqnarray*} \phi(r_+) &=& \frac{1}{4\pi \varepsilon_0} \frac{Q}{\sqrt ...

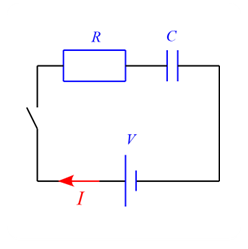
問題 図のようなRC回路を考える。スイッチを入れる前にコンデンサーに電荷は蓄えられていないものとする。時刻$t=0$でスイッチを入れたとして以下の問いに答えよ。 (1) この回路の回路方程式を記述せよ。ある時刻$t$におけるコンデンサーの電荷を$Q(t)$としてよい。 (2) 時計回りの向きを正として、$t=0$における電流$I(0)$を求めよ。 (3) 十分に時間が経った後のコンデンサーの電荷$Q(\infty)$を求めよ。 (4) $Q-t$グラフを描け。また、$Q-t$グラフの原点での傾きを求めよ。 ...

問題 単位長さ当たりの巻き数が$n$である無限長ソレノイドコイルが作る磁場について以下の問いに答えよ。 (1) 中心軸上の磁場$B_{z_n}$を求めよ。 解答 円形電流が作る磁場の結果より円形電流の中心軸上に作られる磁場の大きさ$B_z$は \begin{eqnarray*} B_z &=& \frac{\mu_0 I}{2} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}} \end{eqnarray*} である。この円形電流が重なってソレノイドコイルが形成されると考えると ...

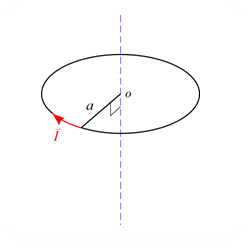
問題 半径$a$の円形電流に時計回りの電流$\vec{I}$が流れている。 この円形電流が作る磁場について以下の問いに答えよ。 (1) 半径$a$の円形電流が中心軸上に作る磁場$B_z$を求めよ。 (2) 半径$a$の円形電流が中心点$o$に作る磁場$B_{z_0}$を求めよ。 解答 (1) 円形電流の微小部分$\diff \vec{s}$を設定し、この微小部分が中心軸上の中心から距離$z$離れた位置に作る磁場を考える。 ベクトル部分を抜き出すと下図のようになる。 ビオーサバールの法則より、 \begin ...

問題 無限に長い直線電流が作る磁場を求めよ。 解答 ビオーサバールの法則より電流の微小部分(電流素片)$I \diff \vec{s}$が点Pの位置に作る磁場$d \vec{B}$は \begin{eqnarray*} \diff \vec{B} = \frac{\mu_0 }{4\pi} \frac{I \diff \vec{s} \times \vec{r}}{r^3} \end{eqnarray*} と表されるので、 直線電流の微小部分が作る電流から距離$R$の位置の磁場の大きさ$\diff B$は ...