平行板コンデンサーの静電容量
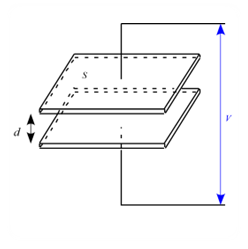
問題 図のような面積 $S$、極板間距離 $d$ の平行板コンデンサーを考える。 ただし、電極間の誘電率は$\varepsilon_0$とする。 (1) 電荷が一様な状態で分布し面密度$\sigma$であるとき電極間の電場$E$を求めよ。 (2) このコンデンサーの静電容量を求めよ。 解答 (1) コンデンサーの両端に$+Q,\ -Q$の電荷を与えるとすると、電荷$Q$は \begin{eqnarray*} Q = \sigma S \end{eqnarray*} で表される。 ガウスの法則は \begi ...
導体表面の電場
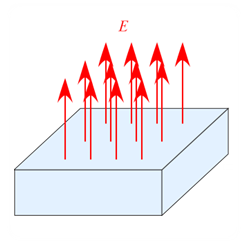
問題 導体の表面に面密度$\sigma$で電荷が分布しているとき、導体表面の電場の大きさ$E$を求めよ。 解答 ガウスの法則は \begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\ \\ \int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\ \end{eqnarray*} となるので 導体の表面において図の様な底面積$\ ...
平行板コンデンサー内のジュール熱
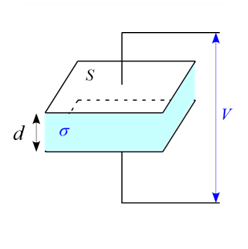
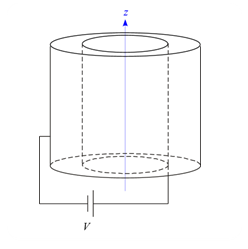
問題 図のような面積 $S$、極板間距離 $d$ の平行板コンデンサーに導体を挿入し、両極板間に電圧 $V$ をかけたとする。ただし、導体の電気伝導率を $\sigma$ とする。以下の問いに答えよ。 (1) 電場$E$を表せ。 (2) 電流密度$i$を表せ。 (3) 電極間に発生する単位時間当たりのジュール熱を求めよ。 解答 (1) 電位$V$と電場$E$の関係は$1 \mbox{C}$当たりの仕事を考えると \begin{eqnarray*} V=E\cdot d \end{eqnarray*} と表 ...
地球の静電容量
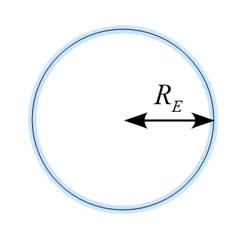
問題 地球を孤立した導体球と仮定し、以下の問いに答えよ。但し、地球の半径は $R_E = 6.38 \times 10^6 \ \mathrm{m}$、真空の誘電率は $\varepsilon_0 = 8.85 \times 10^{-12} \ \mathrm{F/m}$ とする。 (1) 地球の中心からの距離$r\ (> R_E)$における電場$E(r)$を求めよ。 (2) 地球の中心からの距離$r\ (> R_E)$における電位$\phi(r)$を求めよ。 (3) 地球の静電容量$C_E$を求めよ。 ...
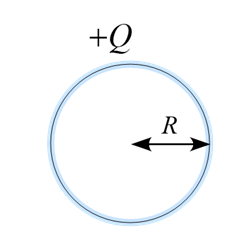
導体球の電場・電位
問題 半径$R$の導体球に電荷$+Q$を与えた。以下の問いに答えよ。 (1) 中心からの距離$r$の電場$E(r)$を求め、$E(r)$のグラフを描け。 (2) 中心からの距離$r$の電位$\phi(r)$を求め、$\phi(r)$のグラフを描け。 解答 ガウスの法則は \begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\ \\ \int \vec{E} \cdot \vec{n} \diff S ...
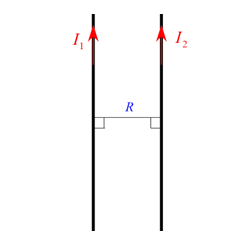
平行な2本の導線が作る磁場による力
問題 平行な2本の導線が距離$R$離れて置かれている。それぞれを流れる電流が$I_1, I_2$としたとき以下の問いに答えよ。 (1) 2本の導線に作用する力の向きを答えよ。 (2) 導線の長さ$L$に働く力を求めよ。 解答 (1) アンペールの法則 \begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\ \\ \mbox{閉曲面$S$の縁$C$に沿っての磁場の ...
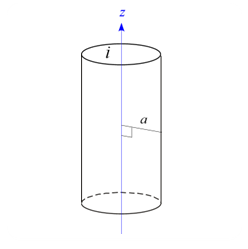
無限に長い円筒に流れる電流が作る磁場
問題 半径 $a$ の無限に長い円筒に定常電流 $i$ が流れているとする。以下の問いに答えよ。ただし、円筒の中心軸を $z$ 軸とする。 (1) 円筒の外側、中心軸からの距離 $r$ が $r > a$ の位置での磁場 $B$ を求めよ。 (2) 円筒の内側、中心軸からの距離 $r$ が $r < a$ の位置での磁場 $B$ を求めよ。 (3) 磁場 $B(r)$ のグラフを描け。 解答 アンペールの法則 \begin{eqnarray*} \oint_C \vec{B} \cdot \diff \v ...
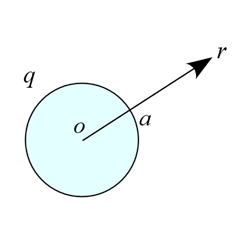
電場中の静電エネルギー密度
問題 真空中に半径 $a$ の金属球があり、電気量 $q$($q > 0$)が帯電しているとする。以下の問いに答えよ。ただし、真空中の静電エネルギー密度は電場 $E$ を用いて次式で表されるものとする。 \begin{eqnarray*} u=\frac{1}{2} \varepsilon_0 E^2 \end{eqnarray*} (1) 金属球の中心から$r\ (r>a)$の位置における電場$E$を求めよ。 (2) 金属球の中心から$r\ (r>a)$の位置における静電エネルギー密度$u(r)$を求め ...
同軸円筒型コンデンサーの静電容量
問題 $z$ 軸を中心軸とし、内側の半径が $a$、外側の半径が $b$ である金属製の筒を用いて、同軸円筒型コンデンサーを考える。ただし、$a < b$ とする。 (1) 2つの筒に電位差 $V$ を与えたとき、単位長さ当たりの電荷 $\rho$ を求めよ。 (2) このコンデンサーの単位長さ当たりの静電容量 $C_L$ を求めよ。 解答 (1) ガウスの法則は \begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\vareps ...
無限に長い円柱の表面に分布した電荷による電場・電位
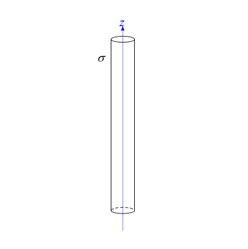
問題 無限に長い半径 $a$ の円柱の表面に、単位長さ当たり $\sigma$ の電荷が帯電しているとする。以下の問いに答えよ。ただし、円柱表面での電位を $\phi_0$ とする。 (1) 電場 $E$ を、円柱の中心からの距離 $r$ の関数として求めよ。 (2) 電位 $\phi$ を、円柱の中心からの距離 $r$ の関数として求めよ。 解答 (1) ガウスの法則は \begin{eqnarray*} \int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\va ...