平行な2本の導線が作る磁場による力

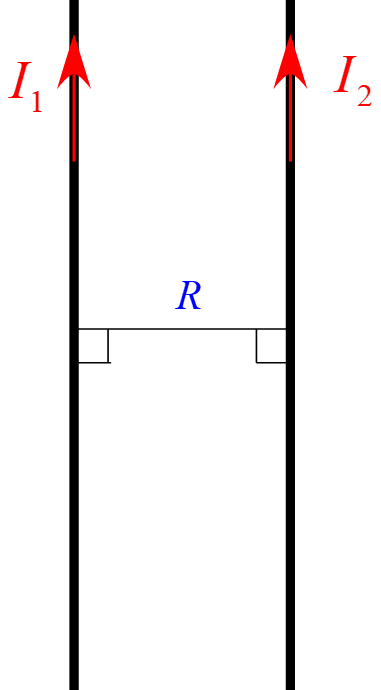
問題

平行な2本の導線が距離$R$離れて置かれている。それぞれを流れる電流が$I_1, I_2$としたとき以下の問いに答えよ。

(1) 2本の導線に作用する力の向きを答えよ。

(2) 導線の長さ$L$に働く力を求めよ。

解答

(1)
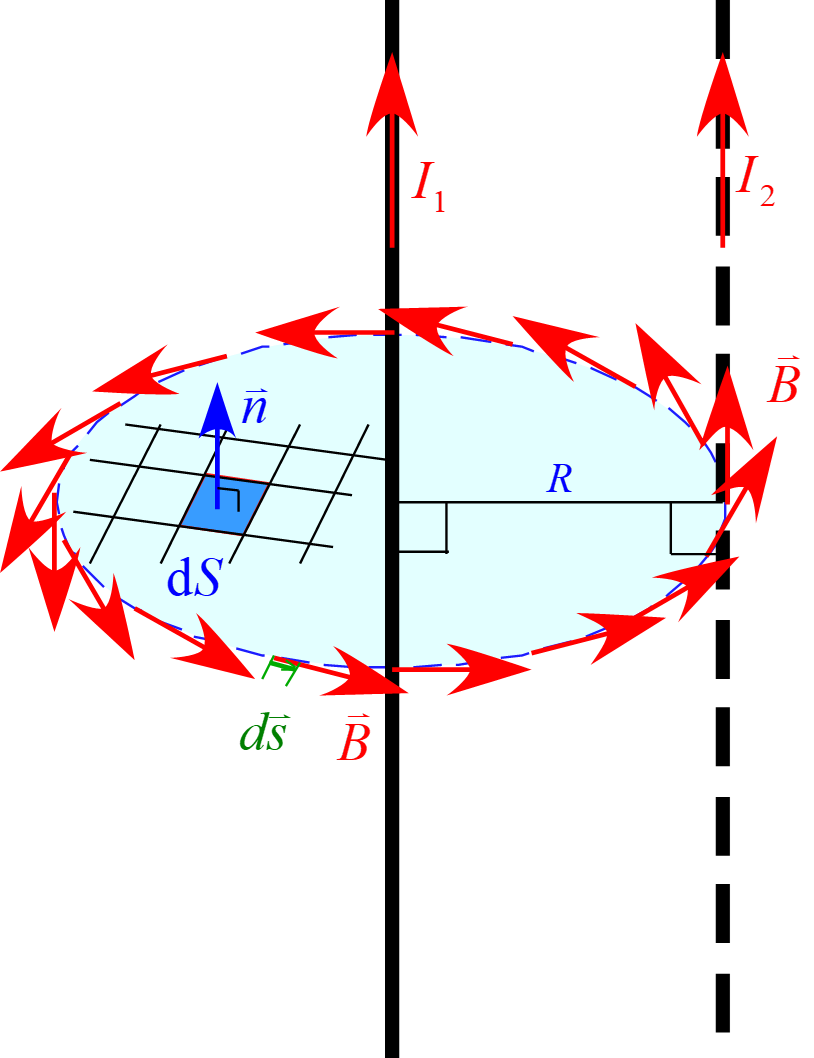
アンペールの法則

$$\begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\ \\ \mbox{閉曲面$S$の縁$C$に沿っての磁場の線積分} &=& \mu_0 \times \mbox{閉曲面$S$を貫く電気量} \end{eqnarray*}$$
より、電流$I_1$が距離$R$だけ離れた位置に作る磁場の大きさ$B_1$は
$$\begin{eqnarray*} \oint_C \vec{B} \cdot \diff \vec{s} &=& \mu_0 \int_S \vec{i} \cdot \diff\vec{S} \\ \\ B_1 \cdot 2\pi R &=& \mu_0 I_1\\ \\ B_1 &=& \frac{\mu_0 I_1}{2 \pi R} \end{eqnarray*}$$
となる。

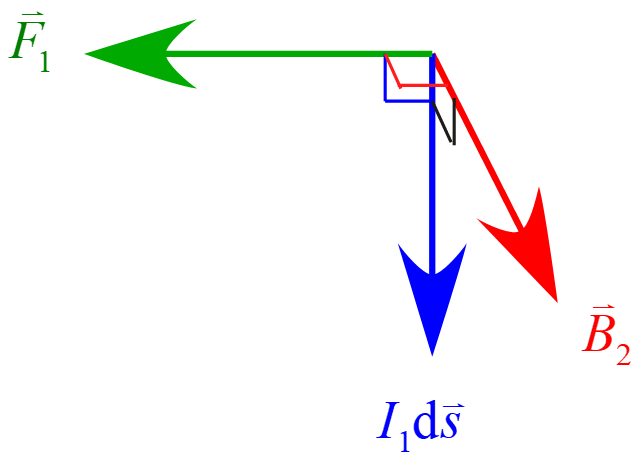
ここでアンペールの力は

$$\begin{eqnarray*} \vec{F}=I \diff \vec{s} \times \vec{B} \end{eqnarray*}$$
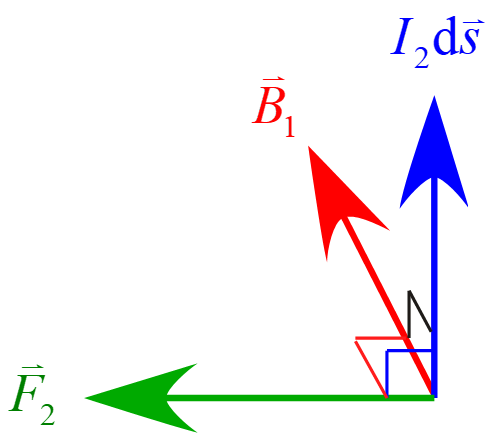
で表され、配置図が図の様になる。

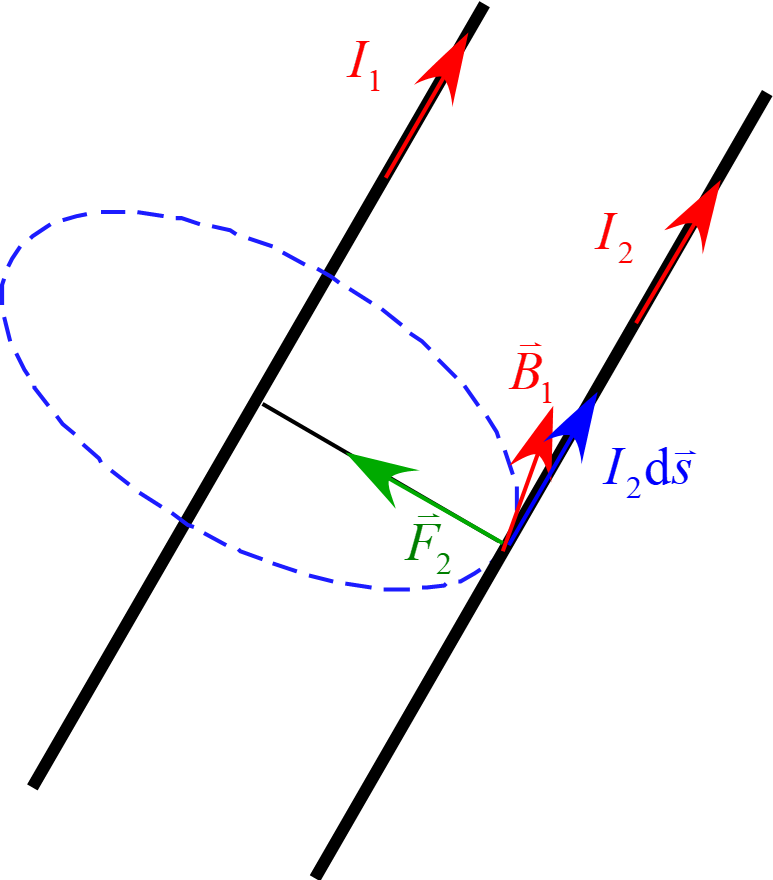
外積の結果である力$\vec{F}_2$は磁場$\vec{B}_1$と電流素片$I_2 \diff \vec{s}$に垂直な方向を向き、磁場$\vec{B}_1$と電流素片$I_2 \diff \vec{s}$のなす角は電流素片$I_2 \diff \vec{s}$から磁場$\vec{B}_1$に向かうので力$\vec{F}_2$は左を向くことになる。

同様に$I_2$を中心に考えると図の様になり、

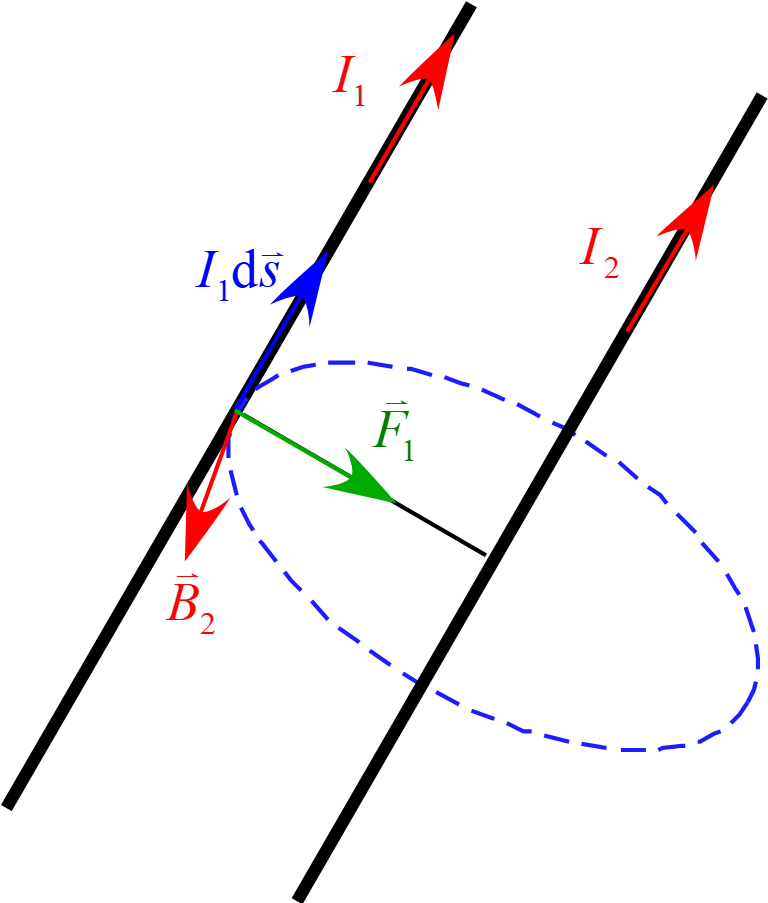
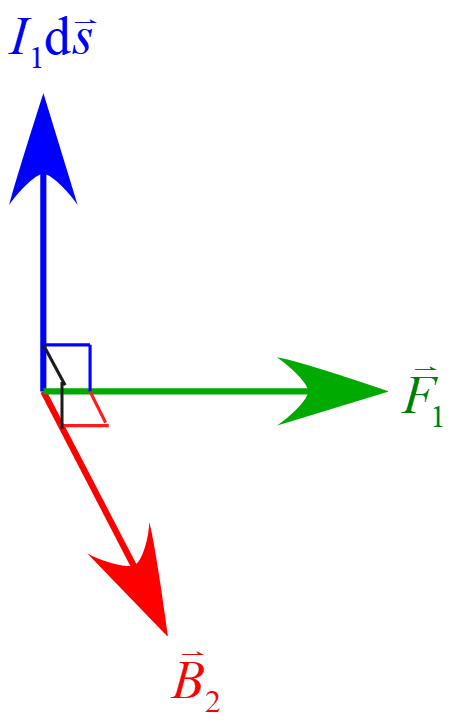
力$\vec{F}_1$は磁場$\vec{B}_2$と電流素片$I_1 \diff \vec{s}$の位置関係は図の様になる。\\

(2)
電流$I_1$が長さ$L$当たりに作用する力の大きさ$|\vec{F}_{L1}|$は

$$\begin{eqnarray*} |\vec{F}_{L1}| &=& |\vec{F}_1| \cdot L\\ \\ &=& |(I_1 \diff \vec{s} \times \vec{B}_2)| \cdot L \\ \\ &=& I_1 |\diff \vec{s}| |\vec{B}_2| \sin \frac{\pi}{2} \cdot L \\ \\ &=& I_1 \cdot 1 \cdot \frac{\mu_0 I_2}{2 \pi R} \cdot 1 \cdot L \\ \\ &=& \frac{\mu_0 I_1 I_2 L}{2\pi R} \end{eqnarray*}$$
となる。
電流$I_2$が長さ$L$当たりに作用する力の大きさ$|\vec{F}_{L2}|$は同様に計算すると

$$\begin{eqnarray*} |\vec{F}_{L2}| &=& |\vec{F}_1| \cdot L\\ \\ &=& |(I_2 \diff \vec{s} \times \vec{B}_1)| \cdot L \\ \\ &=& I_2 |\diff \vec{s}| |\vec{B}_1| \sin \frac{\pi}{2} \cdot L \\ \\ &=& I_2 \cdot 1 \cdot \frac{\mu_0 I_1}{2 \pi R} \cdot 1 \cdot L \\ \\ &=& \frac{\mu_0 I_1 I_2 L}{2\pi R} \end{eqnarray*}$$
となり、同様の結果を得る。

電流の向きが変化する場合

電流$I_1$の向きが逆転すると、電流$I_1$による磁場$\vec{B}_1$の向きが逆転し、電流$I_2$に作用する力の向きが逆転し、右向きに力が作用する。

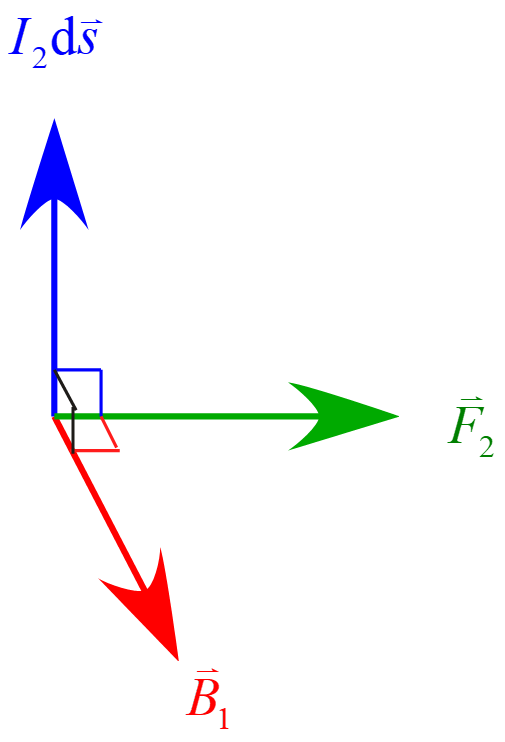
一方、電流$I_1$に作用する力は電流素片$I_1 \diff \vec{s}$の向きが逆転することになるので、図の様になり、左向きに力が作用することになる。