問題
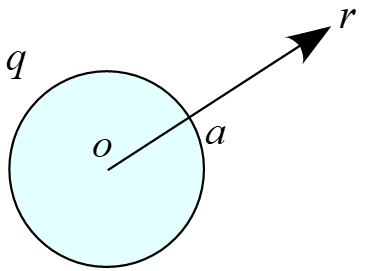
真空中に半径 $a$ の金属球があり、電気量 $q$($q > 0$)が帯電しているとする。以下の問いに答えよ。ただし、真空中の静電エネルギー密度は電場 $E$ を用いて次式で表されるものとする。
\begin{eqnarray*}
u=\frac{1}{2} \varepsilon_0 E^2
\end{eqnarray*}
(1) 金属球の中心から$r\ (r>a)$の位置における電場$E$を求めよ。
(2) 金属球の中心から$r\ (r>a)$の位置における静電エネルギー密度$u(r)$を求めよ。
(3) 全静電エネルギーを求めよ。
解答
(1)
ガウスの法則は
\begin{eqnarray*}
\int \vec{E} \cdot \diff \vec{S} &=& \frac{Q}{\varepsilon_0} \\
\\
\int \vec{E} \cdot \vec{n} \diff S &=& \frac{Q}{\varepsilon_0} \\
\end{eqnarray*}
なので
$a < r$において図の様な半径$r$の球の閉曲面を想定し
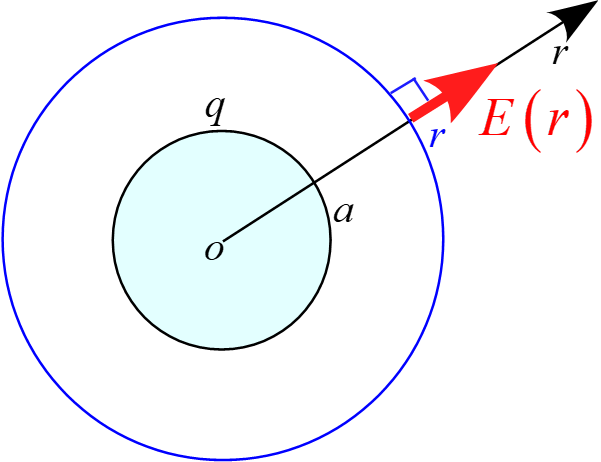
ガウスの法則を適用すると
\begin{eqnarray*}
E(r) \cdot 4 \pi r^2 &=& \frac{q}{\varepsilon_0} \\
\\
E(r) &=& \frac{q}{4 \pi \varepsilon_0} \frac{1}{r^2}
\end{eqnarray*}
となる。
(2)
静電エネルギー密度$u(r)$は
\begin{eqnarray*}
u(r) &=& \frac{1}{2} \varepsilon_0 E^2 \\
\\
&=& \frac{1}{2} \varepsilon_0 \biggl(\frac{q}{4 \pi \varepsilon_0} \frac{1}{r^2}\biggr)^2 \\
\\
&=& \frac{1}{2} \varepsilon_0 \frac{q^2}{4^2 \pi^2 \varepsilon_0^2} \frac{1}{r^4} \\
\\
&=& \frac{q^2}{32 \pi^2 \varepsilon_0} \frac{1}{r^4}
\end{eqnarray*}
となる。
(3)
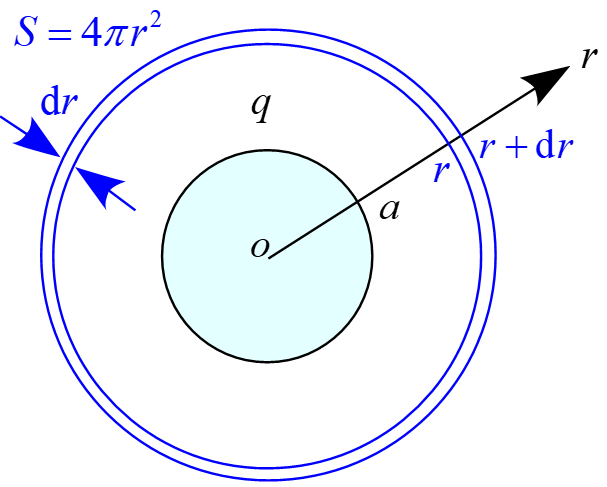
微小な区間$\diff r$の同心球の体積$\diff V$は
\begin{eqnarray*}
\diff V &=& 4\pi r^2 \diff r
\end{eqnarray*}
と表されるのでこの区間内の静電エネルギー$\diff U$は
\begin{eqnarray*}
\diff U &=&u\ 4\pi r^2 \diff r
\end{eqnarray*}
と表される。
従って全区間を計算すると
\begin{eqnarray*}
U &=& \int_a^{\infty} u\ 4\pi r^2 \diff r \\
\\
&=& \int_a^{\infty} \frac{q^2}{32 \pi^2 \varepsilon_0} \frac{1}{r^4} 4\pi r^2 \diff r \\
\\
&=& \frac{q^2}{8\pi \varepsilon_0} \int_a^{\infty} \frac{1}{r^2} \diff r \\
\\
&=& \frac{q^2}{8\pi \varepsilon_0} \biggl[-\frac{1}{r} \biggr]_a^{\infty} \\
\\
&=& \frac{q^2}{8\pi \varepsilon_0} \biggl[-\frac{1}{\infty}
-\biggl( - \frac{1}{a} \biggr) \biggr] \\
\\
&=& \frac{q^2}{8\pi \varepsilon_0 a}
\end{eqnarray*}
となる。