問題
単位長さ当たりの巻き数が$n$である無限長ソレノイドコイルが作る磁場について以下の問いに答えよ。
(1) 中心軸上の磁場$B_{z_n}$を求めよ。

解答
円形電流が作る磁場の結果より円形電流の中心軸上に作られる磁場の大きさ$B_z$は
\begin{eqnarray*}
B_z &=& \frac{\mu_0 I}{2} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}}
\end{eqnarray*}
である。この円形電流が重なってソレノイドコイルが形成されると考えると
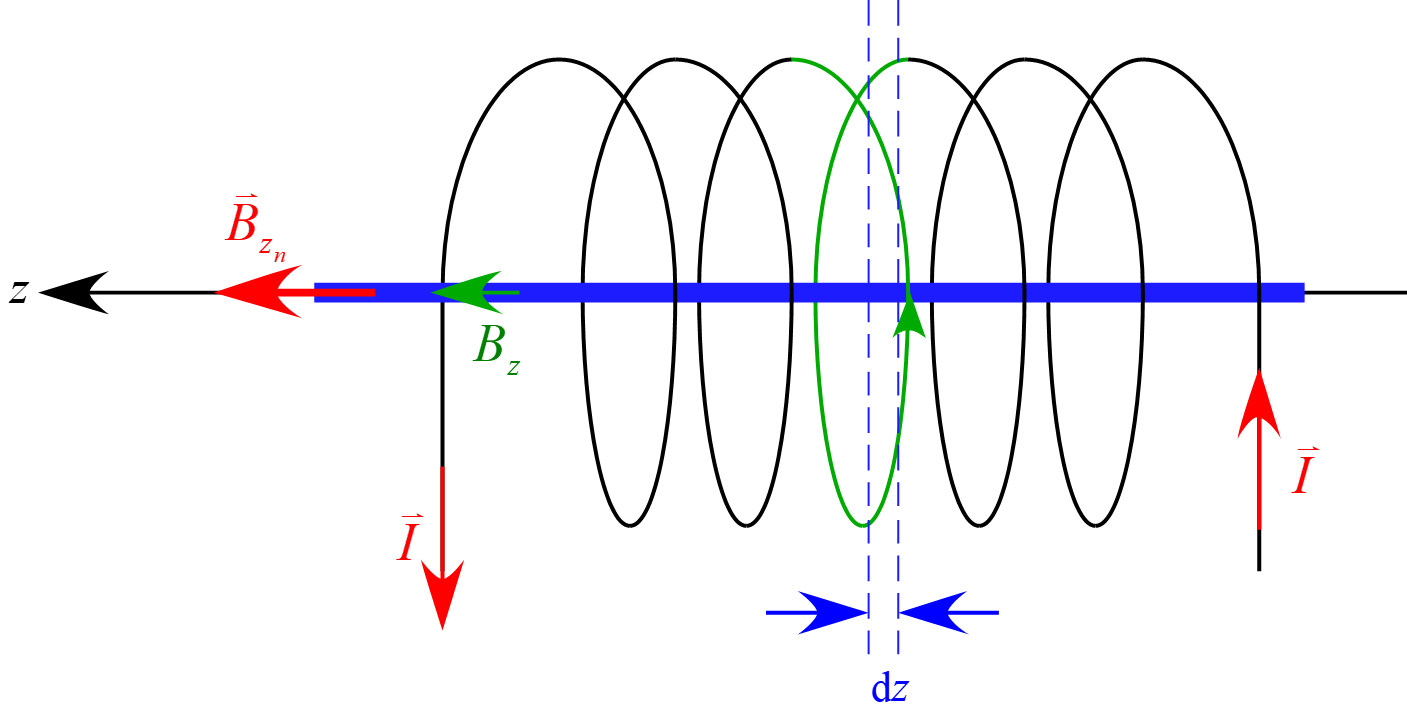
\begin{eqnarray*}
B_{z_n} &=& \int_{-\infty}^{\infty} \frac{n\ \mu_0 I}{2} \frac{a^2}{(a^2 + z^2)^{\frac{3}{2}}} \diff z \\
\\
&=& \frac{n\mu_0 I a^2}{2} \int_{-\infty}^{\infty} \frac{1}{(a^2 + z^2)^{\frac{3}{2}}} \diff z \\
\\
&=& \frac{n\mu_0 I a^2}{2} \frac{2}{a^2}\\
\\
&=& \mu_0 n I
\end{eqnarray*}
となる。
$\displaystyle \int_{-\infty}^{\infty} \frac{1}{(a^2+z^2)^{\frac{3}{2}}} \diff z$の積分について
$z=a \tan \theta$と置換すると
\begin{eqnarray*}
z &=& a \tan \theta \\
\\
\frac{\diff z}{\diff \theta} &=& \frac{\diff}{\diff \theta} (a \tan \theta) = a \frac{1}{\cos^2 \theta} \\
\end{eqnarray*}
よって
\begin{eqnarray*}
\int_{-\infty}^{\infty} \frac{1}{(a^2+z^2)^{\frac{3}{2}}} \diff z
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{(a^2+a^2\tan^2 \theta)^{\frac{3}{2}}} \diff z \\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{[a^2(1+\tan^2 \theta)]^{\frac{3}{2}}} \frac{a}{\cos^2 \theta} \diff \theta\\
\\
&=& \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{a^3(1+\tan^2 \theta)^{\frac{3}{2}}} \frac{a}{\cos^2 \theta} \diff \theta \\
\\
&=& \frac{1}{a^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{(\frac{1}{\cos^2 \theta})^{\frac{3}{2}}} \frac{1}{\cos^2 \theta} \diff \theta \qquad (1+ \tan^2 \theta = \frac{1}{\cos^2 \theta})\\
\\
&=& \frac{1}{a^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1}{\frac{1}{\cos^3 \theta}} \frac{1}{\cos^2 \theta} \diff \theta \\
\\
&=& \frac{1}{a^2} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \theta \diff \theta \\
\\
&=& \frac{2}{a^2}
\end{eqnarray*}
となる。