動く粗い斜面上の物体が滑り出さない条件

問題

滑らかな水平面となす角$\theta$の摩擦のある粗い斜面に、質量$m$の物体を置かれ静止している。斜面を左向きの水平方向に加速度$\alpha$で動かすモデルを考える。
以下の問いに答えよ。但し、静止摩擦係数を$\mu$とする。

(1) 物体の運動方程式を記述せよ。

(2) 物体が斜面を滑り出さない為の斜面の加速度$\alpha$の条件を求めよ。

解答

(1)(2)
斜面の加速度$\alpha$は小さすぎると物体は斜面に沿って滑り降り、大きすぎれば斜面に沿って滑り上がる。従って、上限と下限を探る必要がある。

滑り降りる場合の限界

物体に作用する力は場の力「重力$mg$」と接触力「斜面からの抗力$R$」と慣性力「$m\alpha$」なり、斜面に固定された座標軸$x, y$に沿って成分を分解すると図のようになる。

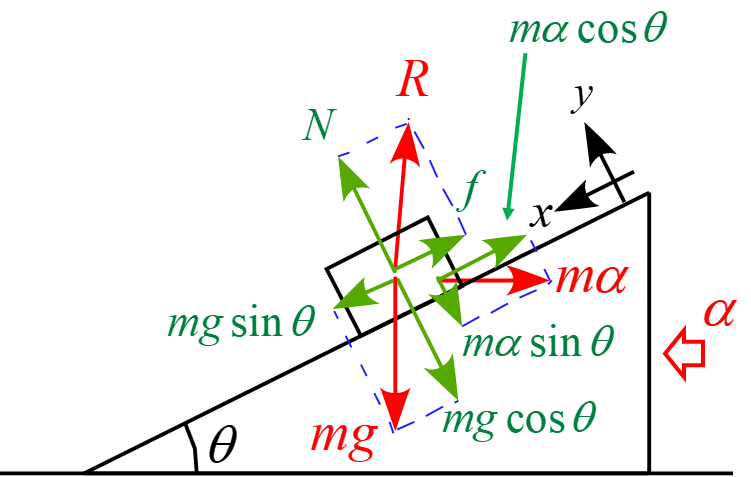
従って、運動方程式は

$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta -f\\ \\ m a_y &=& N - m\alpha \sin \theta - mg \cos \theta \end{eqnarray*}$$
束縛条件は$a_y=0$であり、摩擦力は静止摩擦力$f=\mu N$になるので
$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta -\mu N \\ \\ 0 &=& N - m\alpha \sin \theta - mg \cos \theta \end{eqnarray*}$$
となる。

よって

$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta -\mu N \\ \\ N &=&m\alpha \sin \theta + mg \cos \theta \end{eqnarray*}$$
より
$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta -\mu (m\alpha \sin \theta + mg \cos \theta) \\ \\ \end{eqnarray*}$$
となる。

動かないためには$ma_x \le 0$が必要となるので

$$\begin{eqnarray*} ma_x = mg \sin \theta - m\alpha \cos \theta -\mu m\alpha \sin \theta - \mu mg \cos \theta &\le& 0\\ \\ - \alpha \cos \theta -\mu \alpha \sin \theta &\le& \mu g \cos \theta - g \sin \theta \\ \\ - \alpha (\cos \theta +\mu \sin \theta) &\le& \mu g \cos \theta - g \sin \theta \\ \\ \alpha &\ge& \frac{-\mu \cos \theta + \sin \theta}{\cos \theta +\mu \sin \theta} \ g\\ \end{eqnarray*}$$
となる。

滑り上がる場合の限界

物体に作用する力は場の力「重力$mg$」と接触力「斜面からの抗力$R$」と慣性力「$m\alpha$」なり、斜面に固定された座標軸$x, y$に沿って成分を分解すると図のようになる。

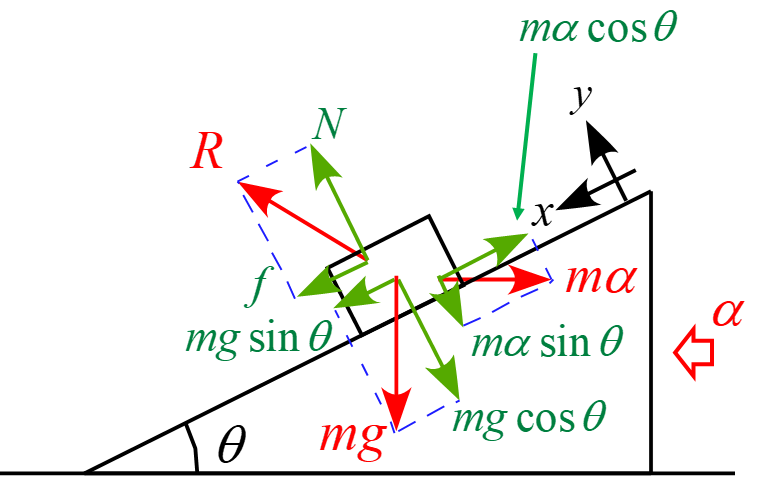
従って、運動方程式は

$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta + f\\ \\ m a_y &=& N - m\alpha \sin \theta - mg \cos \theta \end{eqnarray*}$$
束縛条件は$a_y=0$であり、摩擦力は静止摩擦力$f=\mu N$になるので
$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta + \mu N \\ \\ 0 &=& N - m\alpha \sin \theta - mg \cos \theta \end{eqnarray*}$$
となる。

よって

$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta + \mu N \\ \\ N &=&m\alpha \sin \theta + mg \cos \theta \end{eqnarray*}$$
より
$$\begin{eqnarray*} m a_x &=& mg \sin \theta - m \alpha \cos \theta +\mu (m\alpha \sin \theta + mg \cos \theta) \\ \\ \end{eqnarray*}$$
となる。

動かないためには$ma_x \le 0$が必要となるので

$$\begin{eqnarray*} ma_x = mg \sin \theta - m\alpha \cos \theta +\mu m\alpha \sin \theta + \mu mg \cos \theta &\le& 0\\ \\ - \alpha \cos \theta +\mu \alpha \sin \theta &\le& -\mu g \cos \theta - g \sin \theta \\ \\ \alpha (- \cos \theta + \mu \sin \theta ) &\le& -\mu g \cos \theta - g \sin \theta \\ \\ \alpha &\le& \frac{-\mu \cos \theta - \sin \theta}{-\cos \theta +\mu \sin \theta} \ g\\ \\ \alpha &\le& \frac{\mu \cos \theta + \sin \theta}{\cos \theta -\mu \sin \theta} \ g\\ \end{eqnarray*}$$
となる。

斜面の加速度$\alpha$の条件範囲

斜面の加速度$\alpha$の条件範囲は

$$\begin{eqnarray*} \frac{-\mu \cos \theta + \sin \theta}{\cos \theta +\mu \sin \theta} \ g \le \alpha \le \frac{\mu \cos \theta + \sin \theta}{\cos \theta -\mu \sin \theta} \ g\\ \end{eqnarray*}$$
となる。