問題
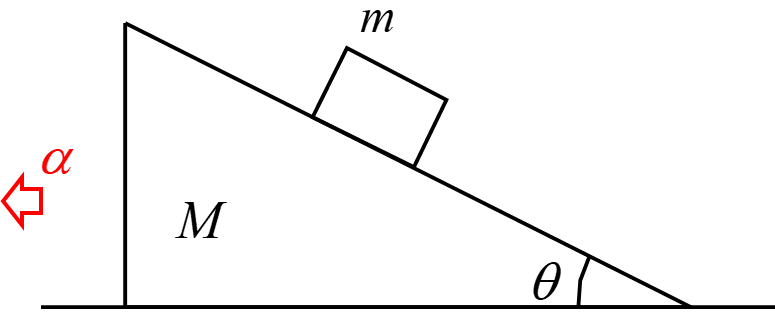
滑らかな水平面となす角$\theta$の質量$M$の滑らかな斜面に、質量$m$の物体を置いたところ、物体は滑り降り、斜面は左向きの水平方向に加速度$\alpha$で動き出した。以下の問いに答えよ。
(1) 斜面と物体の運動方程式を記述せよ。
(2) 斜面の加速度$\alpha$を求めよ。
(3) 斜面上の物体の速度$v_x(t)$を求めよ。
(4) 斜面上の物体の位置$x(t)$を求めよ。
(5) 斜面上を長さ$L$だけ進むのにかかる時間$t_1$を求めよ。
解答
(1)
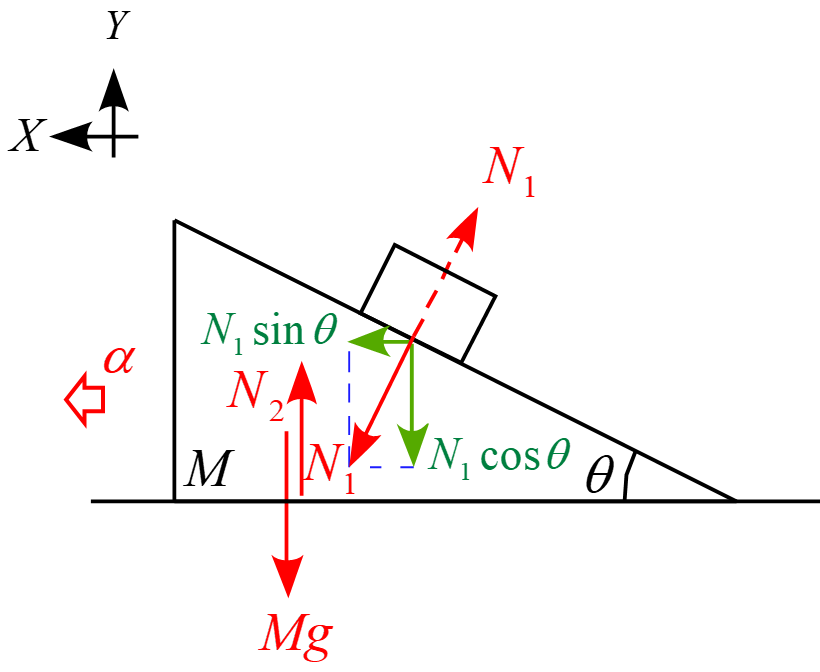
斜面については作用する力は場の力「重力$Mg$」と接触力「斜面に置かれた物体からの抗力$N_1(R_1)$」「床からの抗力$N_2(R_2)$」となり、座標軸$X, Y$に沿って成分を分解すると図のようになる。(注: 床や斜面は滑らかで摩擦力が作用しないため、抗力$R$は床や斜面に垂直な方向にのみ作用し、傾くことはない。)
従って、運動方程式は
\begin{eqnarray*}
M a_X &=& N_1 \sin \theta\\
\\
M a_Y &=& N_2 -Mg - N_1\cos \theta
\end{eqnarray*}
初期条件$a_X=\alpha , a_Y=0$より
\begin{eqnarray*}
M \alpha &=& N_1 \sin \theta\\
\\
0 &=& N_2 -Mg - N_1\cos \theta
\end{eqnarray*}
となる。
物体に作用する力は場の力「重力$mg$」と接触力「斜面からの抗力$(N_1)R_1$」と慣性力「$m \alpha$」となり、座標軸$x,y$に沿って成分を分解すると図のようになる。
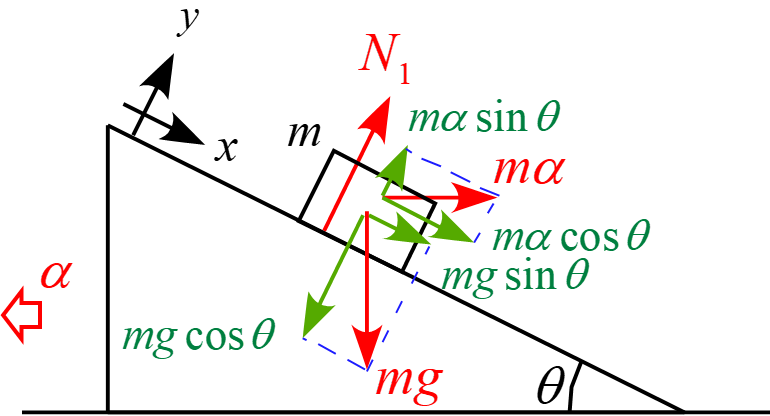
従って、運動方程式は
\begin{eqnarray*}
m a_x &=& mg \sin \theta + m \alpha \cos \theta\\
\\
m a_y &=& N_1 -mg \cos \theta + m\alpha \sin \theta
\end{eqnarray*}
物体は斜面に沿って運動しているので$a_y=0$より
\begin{eqnarray*}
m a_x &=& mg \sin \theta + m \alpha \cos \theta\\
\\
0 &=& N_1 - mg \cos \theta + m\alpha \sin \theta
\end{eqnarray*}
となる。
(2)
(1)の結果$N_1=mg \cos \theta - m\alpha \sin \theta$を斜面の運動方程式に代入すると
\begin{eqnarray*}
M \alpha &=& N_1 \sin \theta\\
\\
M \alpha &=& (mg \cos \theta - m\alpha \sin \theta) \sin \theta\\
\\
M \alpha &=& mg \cos \theta \sin \theta - m\alpha \sin^2 \theta\\
\\
M \alpha + m\alpha \sin^2 \theta &=& mg \cos \theta \sin \theta \\
\\
\alpha(M+ m\sin^2 \theta) + &=& mg \cos \theta \sin \theta \\
\\
\alpha &=& \frac{mg \cos \theta \sin \theta}{M+ m\sin^2 \theta}
\end{eqnarray*}
となる。
(3)
(1)の結果より斜面に沿った運動方程式は
\begin{eqnarray*}
m a_x &=& mg \sin \theta + m \alpha \cos \theta\\
\\
a_x &=& g \sin \theta + \alpha \cos \theta
\end{eqnarray*}
となるので、両辺$t$で積分すると
\begin{eqnarray*}
a_x = \frac{\diff v_x}{\diff t} &=& g \sin \theta + \alpha \cos \theta\\
\\
\int \frac{\diff v_x}{\diff t} \diff t &=& \int (g \sin \theta + \alpha \cos \theta)\ \diff t\\
\\
\int \diff v_x &=& \int (g \sin \theta + \alpha \cos \theta)\ \diff t\\
\\
v_x &=& (g \sin \theta + \alpha \cos \theta)t +C_1 \qquad (C_1:\mbox{積分定数})\\
\end{eqnarray*}
となり、初期条件$v(0)=0$より
\begin{eqnarray*}
v_x (0) = (g \sin \theta + \alpha \cos \theta)\cdot 0 +C_1 &=& 0\\
\\
C_1 &=& 0
\end{eqnarray*}
であるから、斜面上の物体の速度$v(t)$は
\begin{eqnarray*}
v_x (t) &=& (g \sin \theta + \alpha \cos \theta)t\\
\end{eqnarray*}
となる。
(4)
(3)の結果をさらに$t$で積分すると
\begin{eqnarray*}
v_x (t) = \frac{\diff x}{\diff t} &=& (g \sin \theta + \alpha \cos \theta)t\\
\\
\int \frac{\diff x}{\diff t} \diff t &=& \int (g \sin \theta + \alpha \cos \theta)t \diff t\\
\\
\int \diff x &=& \int (g \sin \theta + \alpha \cos \theta)t \diff t\\
\\
x &=& \frac{1}{2}(g \sin \theta + \alpha \cos \theta)t^2 +C_2 \qquad (C_2:\mbox{積分定数})\\
\end{eqnarray*}
であるから、スタート時を原点とすると初期条件$x(0)=0$となり
\begin{eqnarray*}
x (0) = \frac{1}{2}(g \sin \theta + \alpha \cos \theta)\cdot 0^2 +C_2 =0\\
\\
C_2 &=& 0
\end{eqnarray*}
となり、斜面上の物体の位置$x(t)$は
\begin{eqnarray*}
x (t) = \frac{1}{2}(g \sin \theta + \alpha \cos \theta)t^2
\end{eqnarray*}
となる。
(5)
斜面上を長さ$L$だけ進んだ時刻を$t_1$とすると(4)の結果より
\begin{eqnarray*}
x (t_1) = \frac{1}{2}(g \sin \theta + \alpha \cos \theta)t_1^2 &=& L
\\
t_1^2 &=& \frac{2L}{g \sin \theta + \alpha \cos \theta}
\end{eqnarray*}
となる。
ここで、分母$g \sin \theta + \alpha \cos \theta$について計算をすると
\begin{eqnarray*}
g \sin \theta + \alpha \cos \theta &=& g \sin \theta + \frac{mg \cos \theta \sin \theta}{M+ m\sin^2 \theta} \cos \theta \\
\\
&=& g \sin \theta \biggl(1+ \frac{m \cos^2 \theta }{M+ m\sin^2 \theta} \biggr)\\
\\
&=& g \sin \theta \biggl(\frac{M+ m\sin^2 \theta + m \cos^2 \theta }{M+ m\sin^2 \theta} \biggr)\\
\\
&=&g \sin \theta \biggl[\frac{M+ m(\sin^2 \theta + \cos^2 \theta) }{M+ m\sin^2 \theta} \biggr]\\
\\
&=& g \sin \theta \frac{M+ m}{M+ m\sin^2 \theta}\\
\\
&=& \frac{(M+m) \sin \theta}{M+ m\sin^2 \theta}g
\end{eqnarray*}
となるので、
\begin{eqnarray*}
t_1^2 &=& \frac{2L}{\frac{(M+m) \sin \theta}{M+ m\sin^2 \theta}g}\\
\\
&=& \frac{2L(M+ m\sin^2 \theta)}{(M+m) g \sin \theta}\\
\\
t_1 &=& \sqrt{\frac{2(M+ m\sin^2 \theta)}{(M+m) g \sin \theta}L}
\end{eqnarray*}
となる。